第六章液体和气体的性质 6.19幻想和数学

第六章液体和气体的性质 6.19幻想和数学

　　以上是这位小说家告诉我们的话。如果我们检验一下这段对话里的事实，却可以发现这只是些没有根据的幻想。我们不必到地心里去查究这件事情；我们只要预备一支铅笔和一张纸，在物理学领域里做一次小小的旅行。

　　首先让我们算一下，必须下降到多么深，气压才能增加千分之一。正常的气压等于760毫米水银柱的重量。假如我们不是住在空气里，而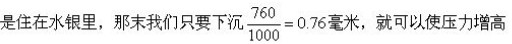千分之一。在空气里，我们当然要下降得更深一些，深度增加的倍数，应当是水银比空气重的倍数，也就是10500倍。所以要使压力比正常气压增加千分之一，我们下降的深度就不会象在水银里那样只下降0.76毫米，而是要下降0.76毫米×10，500，也就是差不多8米。当我们再下降8米的时候，压力又会增大自己的数值的千分之一，依此类推①。总之，我们无论是在哪个高度上在人类上升的最高限上也好（22公里），珠穆朗玛峰的顶上也好（9公里），在海平面上也好都必须下降8米才能使气压比原来的数值增大千分之一。因此，我们就得到这样一个关于空气压力随着深度的增加而增长的表：

　　在地面上，压力760毫米=正常气压

　　在地面下8米深处的压力=正常气压的1.001倍

　　在地面下2×8米深处的压力=正常气压的（1.001）2倍

　　在地面下3×8米深处的压力=正常气压的（1.001）3倍

　　在地面下4×8米深处的压力=正常气压的（1.001）4倍

　　总而言之，在n×8米深处，大气的压力就等于正常压力的（1.001）n倍，并且在压力不十分大的时候，空气的密度也要增加同样的倍数（马里奥特定律）。

　　根据小说里的话，地下旅行家所到的深度不过是48公里，所以重力的减小以及同这种减小有关的空气重量的减小，都可以不必计算。

　　现在就可以计算一下儒勒·凡尔纳的地下旅行家在48公里（48，000米）深处所受到的压力。在我们的式子里

　　这里需要计算的是（1.001）ⁿ。把1.001自乘6000次是一个非常枯燥而且费时的工作。所以我们得利用对数。关于对数，拉普拉斯说得很正确①，它能缩短我们的劳动，因而增加计算的人的寿命。用对数算的时候，我们有这样一个式子：要求的数的对数等于

6000×log1.001=6000×0.00043=2.6。

　　从对数2.6，我们得到了要求的数等于400。

　　所以在48公里的深处，大气的压力是正常气压的400倍。实验告诉我们，在这种压力下空气的密度会增加到原来的315倍。所以我们的地下旅行家说，除了“耳朵痛”以外没有感到任何不舒服，那是很可怀疑的……在儒勒·凡尔纳的小说里，又曾经说到人们到过地下更深的地方120公里，甚至325公里。在那些地方空气的压力应该高到可怕的程度；可是人所能受得住的空气压力，是不能超过3-4个大气压的。

　　利用同一个式子，我们可以计算在多少深的地方，空气的密度会变得象水一样，也就是说密到原来的770倍。得到的数字是53公里。但是这个结果是不可靠的，因为在高压下，气体的密度已经不和压力成正比。马里奥特定律只是在不太高的压力下（一百个大气压以内）才是完全正确的。下面是纳杰列尔实验得到的夫于空气密度的资料。

　　压力 密度

　　200大气压…………………………190

　　400大气压…………………………315

　　600大气压…………………………387

　　1500大气压…………………………513

　　1800大气压…………………………540

　　2100大气压…………………………564

　　从这张表里可以看出，密度的增加是落在压力增加的后面的。所以儒勒·凡尔纳小说里的科学家想在达到某种深度以后，空气的密度会比水的还高，那是白费心思的。是不会有这种情况的，因为空气只有在3000个大气压下，才能同水一样密。在这以后，已经几乎不能再压缩了。要把空气变成固体，单用压力而不同时剧烈降低温度（零下146度），是不可能的。

　　可是为了公道起见，也需要指出，儒勒·凡尔纳的小说是在刚才举出的那些事实发现以前很久出版的。所以这位作者虽然说得不对，也是可以原谅的。

　　让我们再用上面那个式子来计算一下，不会危害在井底工作的人的健康的矿井，最深的应该是多深。我们的身体受得住的最大的空气压力是3个大气压。把需要求得的矿井的深度用x来代表，我们可以得到这个方程式：

　　可以用对数算出x的数值。得出的结果是8.9公里。

　　所以在地面以下大约9公里的深处，人是能不受危害地居住的。

　　 欢迎使用手机、平板等移动设备访问中考网，2024中考一路陪伴同行！>>点击查看