特殊的平行四边形及等腰梯形式四边形的主要内容,它们的应用非常广泛。现就它们的识别条件举例说明,供同学们参考。
一、平行四边形
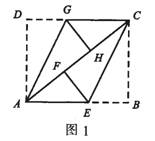
例1 如图1,有一矩形纸片ABCD,翻折∠B、∠D,使BC、AD恰好落在AC上。设F、H分别是B、D落在AC上的点,E、G分别是折痕CE、AG与AB、CD的交点。求证:四边形AECG是平行四边形。
谈特殊四边形的识别
分析:要证明四边形AECG是平行四边形,题中已有条件CG∥AE,因此可考虑证明CG=AE,利用“一组对边平行且相等的四边形是平行四边形”;也可以考虑证明AG∥CE,利用“两组对边分别平行的四边形是平行四边形”。下面用第二种思路证明。
证明:在矩形ABCD中,因为AD∥BC,所以∠DAC=∠BCA。由题意,得∠GAH=
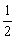
∠DAC,∠ECF=
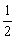
∠BCA,所以∠GAH=∠ECF,所以AG∥CE 。又因为CG∥AE,所以四边形AECG是平行四边形。
点评:平行四边形常见的判定方法还有:①两组对边分别相等的四边形;②对角线互相平分的四边形;③两组对角分别相等的四边形。运用时,要灵活选择。如果一种方法不易解出,可以尝试其他的方法。
二、矩形
例2 如图2,在△ABC中,AB=AC。AD⊥BC,垂足为点D。AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E。求证:四边形ADCE为矩形。
谈特殊四边形的识别
分析:要证明四边形ADCR为矩形,题设中已有两个角是直角的条件,可考虑利用“有三个角是直角的四边形是矩形”来证明,故只要证明∠DAE是直角即可。
证明:在△ABC中,AB=AC,AD⊥BC,所以∠BAD=∠DAC。因为AN是△ABC外角∠CAM的平分线,所以∠MAE=∠CAE。故∠DAE=∠DAC+∠CAE=。

又因为AD⊥BC,CE⊥AN,所以四边形ADCE为矩形。
点评:矩形常见的判定方法有:①三个角是直角的四边形;②有一个角是直角的平行四边形;③两条对角线相等的平行四边形。
三、菱形
例3 如图3,在梯形纸片ABCD中,AD∥BC,AD>CD。将纸片沿过点D的直线折叠,使点C落在AD上的点C1处,折痕DE交BC于点E。求证:四边形CDC1E是菱形。
谈特殊四边形的识别
分析:由于是折叠问题,因此有很多边相等、角相等,可以考虑利用“四条边都相等的四边形是菱形”来证明。
证明:由题意可知△CDE≌△C1DE,则有CD=C1D,∠C1DE=∠CDE,CE=C1E。因为AD∥BC,所以∠C1DE=∠CED。故∠CDE=∠CED,于是CD=CE。所以CD=C1D=C1E=CE,四边形CDC1E是菱形。
点评:菱形常见的判定方法有:①四条边都相等的四边形;②有一组邻边相等的平行四边形;③对角线互相垂直的平行四边形。在折叠问题中,如果有平行线的条件,一般都会有等腰三角形存在。这点应当重视。
四、正方形
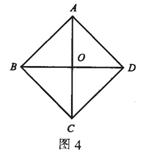
例4 如图4所示,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O。若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加的一个条件是 。
谈特殊四边形的识别
分析:这是一道开放型题目。根据已知条件知四边形ABCD是菱形,要使四边形ABCD是正方形,按其判定方法只要增加条件∠BAD=90°,或∠ABD=45°,或AC=BD等。
解:略。
点评:正方形常见的判定方法有:①有一组邻边相等的矩形;②有一个角是直角的(或对角线相等的)菱形。
五、等腰梯形
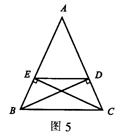
例5 如图5,在等腰△ABC中,AB=AC。BD⊥AC,CE⊥AB,垂足分别为点D、E,连接DE。求证:四边形BCDE是等腰梯形。
谈特殊四边形的识别
分析:要证明四边形BCDE是等腰梯形,首先要证明它是梯形,再证明其两腰相等即可。由图形知BE与CD显然不平行,因此要证明DE∥BC,可通过“同位角相等,两直线平行”来解决。要证明这个梯形是等腰梯形,可通过说明两腰相等的方法达到。
证明:在等腰△ABC中,AB=AC,∠ABC=∠ACB。因为BD⊥AC,CE⊥AB,所以∠BEC=∠CDB=90°。又BC=CB,所以△BEC≌△CDB(AAS)。于是BE=CD。从而AB-BE=AC-CD,即AE=AD。所以∠AED=∠ADE。所以∠ABC=∠AED=
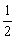
(180°-∠A)。所以DE∥BC。而BE与CD不平行,所以四边形BCDE是梯形。又因为BE=CD,故四边形BCDE是等腰梯形。
点评:等腰梯形常见的判定方法有:①两腰相等的梯形;②同一底上的两个角相等的梯形;③对角线相等的梯形。
新初三快扫码关注
中考网微信公众号
每日推送学习技巧,学科知识点
助你迎接2020年中考!
欢迎使用手机、平板等移动设备访问中考网,2023中考一路陪伴同行!>>点击查看
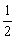 ∠DAC,∠ECF=
∠DAC,∠ECF=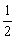 ∠BCA,所以∠GAH=∠ECF,所以AG∥CE 。又因为CG∥AE,所以四边形AECG是平行四边形。
∠BCA,所以∠GAH=∠ECF,所以AG∥CE 。又因为CG∥AE,所以四边形AECG是平行四边形。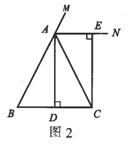
 又因为AD⊥BC,CE⊥AN,所以四边形ADCE为矩形。
又因为AD⊥BC,CE⊥AN,所以四边形ADCE为矩形。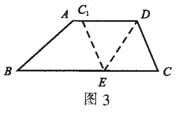
 (180°-∠A)。所以DE∥BC。而BE与CD不平行,所以四边形BCDE是梯形。又因为BE=CD,故四边形BCDE是等腰梯形。
(180°-∠A)。所以DE∥BC。而BE与CD不平行,所以四边形BCDE是梯形。又因为BE=CD,故四边形BCDE是等腰梯形。