梯形是一种特殊的四边形,它是平行四边形和三角形的“综合”。可以通过适当地添加辅助线,构造三角形、平行四边形,再运用三角形、平行四边形的相关知识去解决梯形问题。下面就梯形中作辅助线的常用方法作一介绍,供参考。
一、 平移一腰
过梯形的一个顶点作一腰的平行线,构造一个三角形和一个平行四边形,能使分散的条件集中起来,为解决梯形问题创造条件。
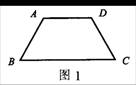
例1 如图1,等腰梯形ABCD两底之差等于一腰的长,那么这个梯形较小的一个内角是( )
A、90° B、60° C、45° D、30°
解析:由条件“两底之差等于一腰的长”,可平移一腰。如图2所示,平移DC到AE,AE交BC于E。可知BE=BC-AD=AB。又AB=DC=AE,故AB=BE=AE,△ABE是等边三角形。所以∠B=60°。故选B。
二、平移两腰
平移两腰,使两腰交于短底上一点,把梯形转化为两个平行四边形和一个三角形,进而解决问题。
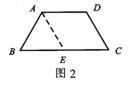
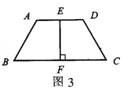
例2 如图3,在梯形ABCD中,AD∥BC,AD<BC。E、F分别为AD、BC的中点,且EF⊥BC。求证:∠B=∠C。
解析:要证∠B=∠C,可把它们移到同一个三角形中,利用等腰三角形的有关性质加以证明。
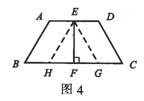
过点E作EH∥AB,EG∥DC,分别交BC于H、G(如图4)。
∵AD∥BC,∴四边形ABHE和四边形EGCD都是平行四边形(两组对边平行)。
∴AE=BH,ED=GC。
又E、F分别为AD、BC的中点,所以AE=ED,BF=FC。
∴BH=GC,BF-BH=FC-GC,从而HF=FG。
又EF⊥BC,所以EH=EG,故∠EHF=∠EGF,得∠B=∠C。
评析:题目中若有连接两底上点的线段,通常要平移两腰。
三、平移对角线
过梯形底边的一个端点作某一条对角线的平行线,可以构造出一个三角形和一个平行四边形,引出解题思路。
例3 在梯形ABCD中,AD∥BC,对角线AC⊥BC,且AC=5cm,BD=12cm,则梯形中位线的长等于( )
A、7.5cm B、7cm C、6.5cm D、6cm
解析:由对角线垂直,可平移一条对角线(比如AC),构造出Rt△BDE和
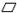
ACED(如图5)。由勾股定理可知BE=13cm,从而得到梯形中位线的长
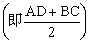
等于BE的一半,即为6.5cm。故选C。
四、延长两腰
延长两腰相交于一点,可构造两个三角形,再利用这两个三角形的性质解决问题。
例4 在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD+BC=30,BD平分∠
ABC。求梯形的周长。
解析:延长两腰相交于点E,如图6,因∠ABC=∠BCD=60°,故∠E=60°。△BCE为等边三角形。又BD平分∠ABC,所以BD垂直平分CE。
所以CD=。
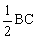
又AD∥BC,故△ADE为等边三角形。AD=ED=CD。由AD+BC=30,知CD+2CD=30,CD=10。
∴梯形的周长为30+AB+CD=30+2CD=50。
五、作梯形的高
过梯形短底的两个端点作梯形的高,把梯形分成两个直角三角形和一个矩形,可使解题思路明朗化。
例5 已知等腰梯形的一个内角为60°,它的上底是3cm,腰长是4cm,则下底是 。
解析:如图7,梯形ABCD中,∠B=∠C=60°,AD=3cm,AB=DC=4cm,过点A、D分别作AE⊥BC,DF⊥BC,垂足分别为E、F。则有∠BAE=∠CDF=30°,BE=FC=
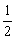
AB=2cm,
∴BC=BE+EF+FC=BE+AD+FC=7(cm),即为所求。
六、连接两腰中点
若题目中有一个或两个腰的中点,可尝试连接梯形两腰的中点,得到梯形的中位线,利用中位线的性质解题。
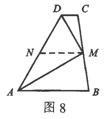
例6 在梯形ABCD中,AB∥CD,点M为BC的中点,DM平分∠ADC。求证AM平分∠DAB。
解析:如图8,取DA的中点N,连接MN,则MN∥CD,MN∥AB。所以∠NMD=∠MDC=∠MDN。故NM=ND=AN,∠NAM=∠NMA=∠MAB。故AM平分∠DAB。
练习
1、等腰梯形两底差的一半等于它的高,那么这个梯形的一个内角是( )。
A、75° B、60° C、45° D、30°
2、如图9,已知梯形ABCD中,AB∥CD,∠A+∠B=90°,M、N分别是AB、CD的中点。求证:MN=
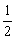
(AB-CD)。
2020年数学学习方法:谈梯形辅助线的作法
3、在梯形ABCD中,AD∥BC,AD=2,BC=8,AC=6,BD=8,求此梯形的高。
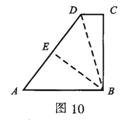
4、如图10,在梯形ABCD中,∠DCB=90°,AB∥DC,AB=25,BC=24。将该梯形折叠,点A恰好与点D重合,BE为折痕。那么,AD的长为 。
2020年数学学习方法:谈梯形辅助线的作法
5、例6变式练习:条件不变,结论改变。求证:(1)AM⊥DM;(2)AB+CD=AD。
提示:1、利用第五种作法。2、利用第二种作法,并利用直角三角形斜边上的中线等于斜边的一半。3、利用第三种作法,由勾股定理逆定理得出直角三角形,并利用面积公式
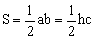
(a、b为直角边长,c为斜边长,h是斜边上的高)。4、先在Rt△BCD中求出DC,再自D作DF⊥AB于F。在Rt△ADF中求AD。
新初三快扫码关注
中考网微信公众号
每日推送学习技巧,学科知识点
助你迎接2020年中考!
欢迎使用手机、平板等移动设备访问中考网,2023中考一路陪伴同行!>>点击查看
 ACED(如图5)。由勾股定理可知BE=13cm,从而得到梯形中位线的长
ACED(如图5)。由勾股定理可知BE=13cm,从而得到梯形中位线的长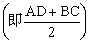 等于BE的一半,即为6.5cm。故选C。
等于BE的一半,即为6.5cm。故选C。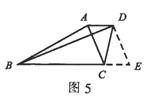
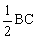 又AD∥BC,故△ADE为等边三角形。AD=ED=CD。由AD+BC=30,知CD+2CD=30,CD=10。
又AD∥BC,故△ADE为等边三角形。AD=ED=CD。由AD+BC=30,知CD+2CD=30,CD=10。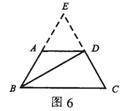
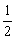 AB=2cm,
AB=2cm,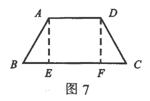
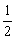 (AB-CD)。
(AB-CD)。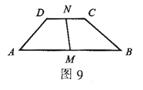
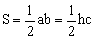 (a、b为直角边长,c为斜边长,h是斜边上的高)。4、先在Rt△BCD中求出DC,再自D作DF⊥AB于F。在Rt△ADF中求AD。
(a、b为直角边长,c为斜边长,h是斜边上的高)。4、先在Rt△BCD中求出DC,再自D作DF⊥AB于F。在Rt△ADF中求AD。