一、一次函数的概念
若两个变量像x、y的关系,可以表示成:y=kx+b(k,b为常数,且k≠0)的形式;那么y就叫做x的一次函数;其中,x是自变量,y是因变量。
1.一次函数的解析式的形式是y=kx+b,判断一个函数是否是一次函数,就是判断是否能化成以上形式。
2.当b=0,k≠0时,y=kx 仍是一次函数。
3.当b=0,k=0时,它不是一次函数。
4.正比例函数是一次函数的特例,一次函数包括正比例函数。
二、一次函数的图象和性质
1. 图象
2. 性质
①在一次函数上的任意一点P(x,y),都满足等式:y=kx+b。
②直线 y=kx+b与y轴的交点是(0,b),与x轴的交点是
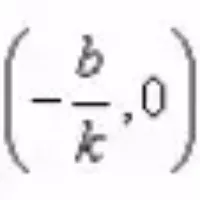
③正比例函数的图象总是过原点。
三、正比例函数与一次函数之间的关系
一次函数y=kx+b的图象是经过(0,b)和
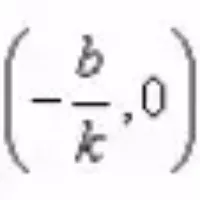
两点的一条直线,我们称它为直线y=kx+b,它可以看作由直线 y=kx平移 |b| 个单位长度得到。(当b>0时,向上平移;当b<0时,向下平移)
四、用待定系数法确定函数解析式的一般步骤
已知点A(x₁,y₁),B(x₂,y₂),请确定过点A,B的一次函数的表达式。
(1)设一次函数的表达式(也叫解析式)为y=kx+b。
(2)因为在一次函数上的任意一点P(x,y),都满足等式 y=kx+b。所以可以列出2个方程:
y₁=kx₁+b…....①
y₂=kx₂+b.......②
(3)解这个二元一次方程,得到k、b的值。
(4)最后得到一次函数的表达式。
五、直线的平移
直线 y=kx+b 向上平移 m(m>0)个单位长度得到直线y=kx+b+m;
直线 y=kx+b 向下平移 m(m>0)个单位长度得到直线 y=kx+b-m;
直线 y=kx+b 向左平移 m(m>0)个单位长度得到直线 y=k(x+m)+b;
直线 y=kx+b 向右平移m(m>0) 个单位长度得到直线y=k(x一m)+b。
直线平移的规律用八字口诀来形象表示:上加下减,左加右减。
六、直线y=k?x+b?(k?≠0)与y=k?x+b?(k?≠0)的位置关系
(1)两直线平行,可得 k?=k? 且 b?≠b?
(2)两直线相交,可得 k?≠k?
(3)两直线重合,可得 k?=k? 且 b?=b?
(4)两直线垂直,可得 k?k?= -1
七、常用公式
欢迎使用手机、平板等移动设备访问中考网,2025中考一路陪伴同行!>>点击查看