2022年初中几何学习方法

初中几何一直是不少同学比较头疼的问题。在证明几何题时，找不准方向，以至于千头万绪，不知从何入手;甚至以前做过的题，也如过眼云烟。

这是什么原因?

我认为是没有掌握数学学习的方法。在这里我先简单的介绍下我自己的数学学习情况(你们也可以理解为我适当的吹嘘下自己)：小学和初中数学每次考试要么是满分要么是接近满分;高中正好遇到我的青春叛逆期，数学成绩有所下滑;但到了大学以后，数学成绩又突飞猛进;研究生招生考试，数学考了139分(满分150，139在当年真算的上是很高的分数，周围很多平时成绩很好的同学连90分都没有)的好成绩;2019年参加高中教师资格证考试，一次性通过(当时有一个87人考初高中数学教师资格证的微信群，仅三人通过，另外两个通过的是初中教师资格证)，要知道这离我2008年硕士毕业，已经11年过去了。11年没看过数学，一次性通过高中数学教师资格证考试(含初中、高中、大学内容)，是什么概念?是因为我数学基础扎实稳固，11年都没怎么忘记。也就是说只要您学习方法得当，真正理解了数学概念，即使过再久捡起来也非常容易。

好，转回正题。

几何不仅仅是初中数学的重点，在高中数学中也占有相当大的比重，其难度呈螺旋式上升，所以初中几何基础一定要打好。好在初中几何变化并不多，大同小异，只要掌握了学习或思考的方法，小的差异举一反三，大多数几何题便迎刃而解。

学好数学不妨分为以下几步，如果你能读懂并执行，90%的题目能一分钟之内甚至几秒钟之内出解题思路，相信你的数学成绩会有质的飞跃!

第一步：牢记概念、定理、性质

很多家长、老师只知道让自己孩子或学生多刷题，实行题海战术，但是他们不清楚自己的孩子甚至连课本上的基本概念都稀里糊涂。一味的做题，把孩子弄得身心俱疲不说，甚至会产生抵触情绪。到最后依然只会做些简单的题目，对于较难的题目，只要稍微有些变化，依然不会，这样会使孩子逐渐失去对数学学习的兴趣。说实话，这样的家长和老师不在少数。

其实大部分看似较难的题目都是从基本的定义、定理和性质入手，不信?一会举几个例子你看看就知道了。

那么如何才能熟练的掌握这些最基本的知识呢?我认为需要做好以下三点：1、熟读教材，理解这些概念的代数和几何意义;2、熟背定义定理性质(谁说数学不用背的?虽说不像语文英语背的那么多，当然不是死记硬背，而是在理解的基础上去背诵);3、做题的过程中要清楚每一题应用了什么概念定理和性质。

如果能牢记并掌握概念、定理、性质，做到以上三点，那么恭喜你，你达到了及格线，也就是说考试满分100分，你能得个60分是不成问题的。

初中几何

当然我们绝大部分同学不满足60分的及格成绩，那怎么办?不急，我们继续看第二步：

第二步：如何去思考?

很多学生碰到较为灵活或稍有难度的题目，千头万绪，百思莫解。这其实是因为没有抓住初中几何的本质，以及思考的方法。实际上很多题压根就不用你怎么去思考，只要你掌握了一个固定的解题方法。

我们先来了解初中几何的本质——初中阶段的大多数数学几何题，本质上都是对线或角之间关系的处理。记住，再强调一遍：线或角(线与线、线与角、角与角)之间关系的处理。

也就是说，如果在解题的过程中，有意识地去找与条件或结论相关的角或线的关系，越多越好，思路通常很快自然而然就出来了。一般情况下，解题时需要先找出突破口，突破口在哪?就是题目中的关键语句。

好，我们来看下面这道例题：

例1、如图，在平行四边形ABCD中，E是AB上一点，DE、CE分别是∠ADC、∠BCD的平分线.若AD=5，DE=6，则平行四边形ABCD的面积是()

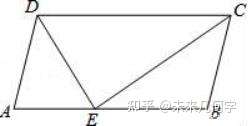
例1 图1-1

A.96 B.60 C.48 D.30

【思考】这一题是让我们求平行四边形ABCD的面积。我们最容易想到是公式法： 底×高;第二种方法：也可以转化为几个三角形的面积和，而求三角形的面积公式是底×高÷2。看看这两种方法本质上都是线与线的关系。

那我们就沿着这条主线转化题目中的每个条件：我们看到条件中关键语句是角平分线，那么我们不用去思考，直接就利用角平分线的性质，把所有相等的角标记出来。有同学也许会问，我们求的是线与线的关系，标出相等的角有什么用?原因在于：一、题目中最关键的语句只有角平分线，我们只有利用角平分线的性质不是?二、角的关系很多时候都可以转化成线与线的关系啊，最常用的等腰三角形两腰相等不是吗?

好，利用角平分线的性质，我们在图中标出ED将∠ADC分为两个相等的∠1，EC将∠DCB分为两个相等的∠2。那么这样我们是否把所有相等的∠1和∠2都标出来了?显然不是!因为我们可以看到只标出这两对相等的角没有用，还是解不出来。那么我们认真读一下题目条件，发现可以再根据平行四边形两对边平行的性质，标出图中所有与∠1和∠2相等的角。

那这与平行四边形面积有什么关系呢?我们再根据刚才求得相等的角转化成线段与线段的关系，很容易看出△ADE和△BCE为等角三角形，即AD=AE=5、BE=BC=5。从而继续求得AB=10，再利用勾股定理或者等面积法求得△ADE的AE边上的高(也为平行四边形的高)，从而求得平行四边形的面积，详细请看本题解法一。

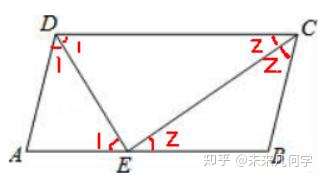
例1 图1-2

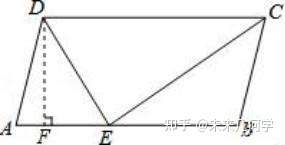
例1 图1-3

方法一：过点D作DF⊥AB于点F，

∵DE、CE分别是∠ADC、∠BCD的平分线， (首先从关键语句角平分线入手)

∴∠ADE=∠CDE，∠DCE=∠BCE，

∵四边形ABCD是平行四边形，

∴AB∥DC，AD=BC=5，

∠CDE=∠DEA，∠DCE=∠CEB， (再利用平行线的性质，找出所有相等的角)

∴∠ADE=∠AED，∠CBE=∠BEC， (等量代换，找出等腰三角形)

∴DA=AE=5，BC=BE=5， (把角的关系转化成角的关系)

∴AB=10，

则DF=DE﹣EF=AD﹣AF，

故6﹣FE=5﹣(5﹣EF)，

解得：EF=3.6，

则DE==4.8，

故平行四边形ABCD的面积是：4.8×10=48.

故选：C.

方法二：当标出所有相等的角以后根据平行四边形的性质，我们发现∠1+∠2=90，那么∠DEC=90;因为DC=AE+EB=10,DE=6，解得：CE=8;所以平行四边形面积为2倍直角三角形DEC的面积，即48。

本题用到了角平分线、平行四边形、平行线、等腰三角形、勾股定理等的基本性质。看到没，这就说明了第一步，熟记定义、定理和性质有多么重要!但显然，本题中最重要的一个条件是角平分线，我们甚至可以不管结论要求什么，而直接由角平分线的性质引导标出所有相等的角。

掌握了第二步如何去思考，100分的试卷，75分以上是不成问题了，那如何才能获取更高分呢?要善于去归纳总结。

第三步，学会如何去归纳总结

做完了一个较难或者你认为比较重要的题目时，记得去归纳总结，形成自己的方法体系。如此，以后再遇到类似的题目时，你可以很快有解题思路。那么怎么去总结归纳呢?我们常用的有：理论知识点归纳法，具体解题方法归纳法。(最好有几个精致的错题本。为什么是几个?因为可能原来的归纳比较浅显，随着学习的进行和深入，后面的归纳会越来越简练、全面、深刻)

3.1、理论知识点归纳法

即我们做一道题，可能要用到哪些相关的知识才能解答出来。比如几何题中求线段最小值，我们学过的关于求线段最小值的定义、定理或性质可以归纳在一起有：

1) 两点之间线段最短;

2) 点到直线的距离垂线段最短;

3) 三角形两边之差小于第三边，两边之和大于第三边。

我们再来举个例子，看一看。

例2、如图，在Rt△ABC中，∠B=90°，AB=3，BC=4，点D在BC上，以AC为对角线的所有ADCE中，DE最小的值是(　　)

A.2 B.3 C.4 D.5

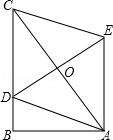
例2 图2-1

【思考】结论要求线段最小值，那我们脑海中就要浮现出，求线段最小值有以上三种定理可以应用。那么本题要用哪个定理呢?我们继续分析：

我们找出题目中的关键语句：以AC为对角线的所有ADCE中。我们知道平行四边形的对角线互相平分，求DE最短，也就是求DO最短，那么当DO什么时候最短呢?O点和BC都是固定的，那么只有当OD⊥BC时，由垂线段最短可知，此时，DO最短，也即DE线段取最小值.

很多同学看到别人的解析，觉得自己懂了，就扔掉不管了。不要以为看到解析，你就真懂了。如果这道题目你开始没做出来，或者解题时千头万绪，花了很长时间才做出来，那么这个时候你就要去归纳了，把它内化成自己的东西。

怎么归纳呢?

首先在错题本上列出几何题中求线段的最小值，相关的定义、定理和性质(上面已列出，此处不再重复)然后再把每种情况下面都对应写个几道例题，方便我们复习时对照着去思考。

3.2、具体方法归纳法

即我们做某一类题，需要用到什么方法?比如我们碰到中点、角平分线等等怎么去做辅助线?看到30、45、60特殊角，或者特殊值时，我们首先应该联想到什么?或者首先要做什么?

我们再来看一道题：

例3、在Rt△ABC中，∠C=90°，AD平分∠CAB，BE平分∠ABC，AD、BE相交于点F，且AF=4，EF=，则AC=——

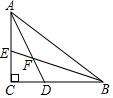
图 例3-1

【思考】看到题目中有线段长为，我们就可以以此来判断是否有以此线段为一边的特殊角为45呢?如果有，我们就可以以此边为直角三角形的斜边构造直角三角形。我们首先来看题目中的关键语句：AD平分∠CAB，BE平分∠ABC，AD、BE相交于点F。有两条角平分线交于一点时，常连接第三个顶点与角平分线的交点;并观察三角形两角和的一半是否为特殊角，很显然，∠FAB+∠FBA=45°，所以由外角定理可得∠AFE=45° 。然后再以EF为斜边构造直角三角形，即过E作EGAD于点G。

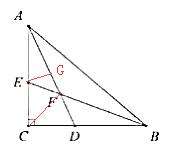
图 例3-2

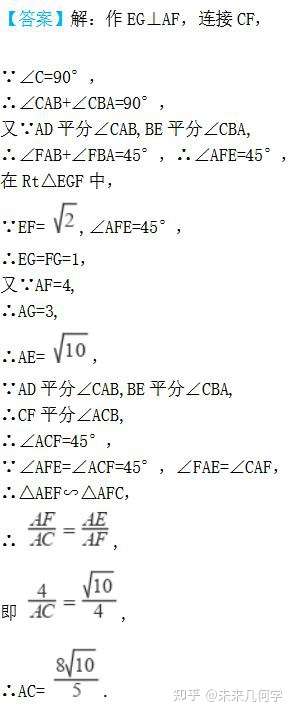
那么通过这个题目我们就可以归纳总结出一个方法：

看到题目中有线段长为、等特殊值时，我们就可以以此来判断是否有以此线段为一边的45、60的特殊角。如果有，我们就可以以此边为直角三角形的斜边或直角边来构造直角三角形。

......

看到没，总结多了，形成自己的知识体系，时常温故而知新，下次再碰到这类题目，就会形成条件发射，下笔如有神!

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看