2023年初中数学锐角三角函数基本应用

三角函数是沟通代数与几何的一座桥梁，代几结合是中考数学必考的重要考察内容之一。　　因此我们必须认真掌握好三角函数的应用。

今天，我们就来学习锐角三角函数在基本平面图形中的综合应用。其中，基本平面图形包括：三角形，四边形(正方形、矩形、棱形)，圆，一次函数、二次函数、双曲线。只有我们熟悉并了解了锐角三角函数在各种基本平面图形中的情况，才能够熟练应用锐角三角函数解决各种相关问题。

而要应用锐角三角函数，我们必须要以直角三角形为依托，如果图形中没有与该锐角直接相关的直角三角形，那我们就要想办法构造与该锐角相关的直角三角形。

​

一、锐角三角函数与三边形

例1、如图，△ABC中AB=AC=4，∠C=72°，D是AB中点，点E在AC上，DE⊥AB，则cosA的值为(　　)

二、锐角三角函数与四边形

2.1、锐角三角函数与矩形

例2、(2016·东营中考)如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知

2.2、锐角三角函数与棱形

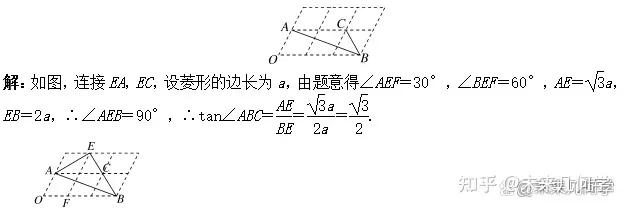
例3、(2016·福州中考)如图，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点.已知菱形的一个角(∠O)为60°，A，B，C都在格点上，则tan∠ABC的值是________.

2.3、锐角三角函数与含直角的一般四边形

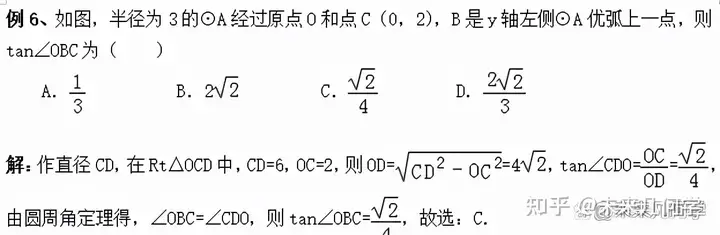
三、锐角三角函数与圆

例5、如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C，

三、　锐角三角函数与函数

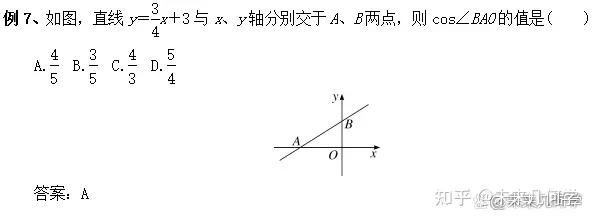
3.1、锐角函数与一次函数

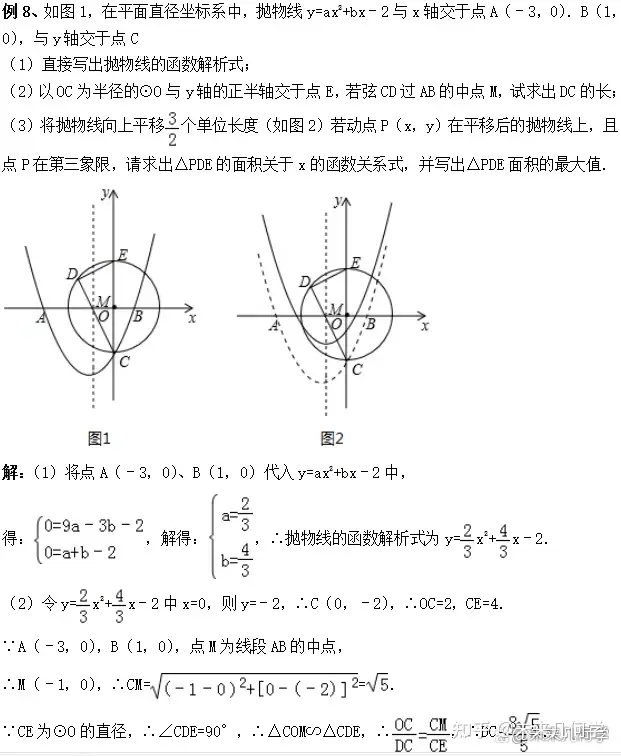
3.2、锐角函数与二次函数

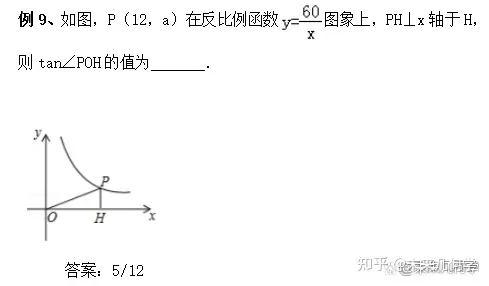
3.3、锐角三角函数与双曲线

　　 欢迎使用手机、平板等移动设备访问中考网，2024中考一路陪伴同行！>>点击查看