来源:网络资源 2022-10-14 13:28:25
以下是其基本概念和图像上特殊点。
常见三种形式。
(其中两根式当二次函数和x轴没有交点的时候不存在,此时可以采用更为一般的 对称点式 ,相当于函数 和直线y=m的两个交点,m为足够大的数)
其中出现过的字母有
a:二次项系数,在三个表达式中都出现过。代表开口大小。
b:一般式的一次项系数。
c:常数项系数
h:顶点式中顶点x坐标
k:顶点式中顶点y坐标
(此处会注意到为什么h前面是有负号,而k前面没有,如有疑惑,请看下面链接)
x_1: 两根式其中一个根
x_2:两根式其中另一个根
以下我以开口向上且和x轴有两个根的二次函数为例,介绍下三个表达式的联系以及适用范围。
如下图为例子:
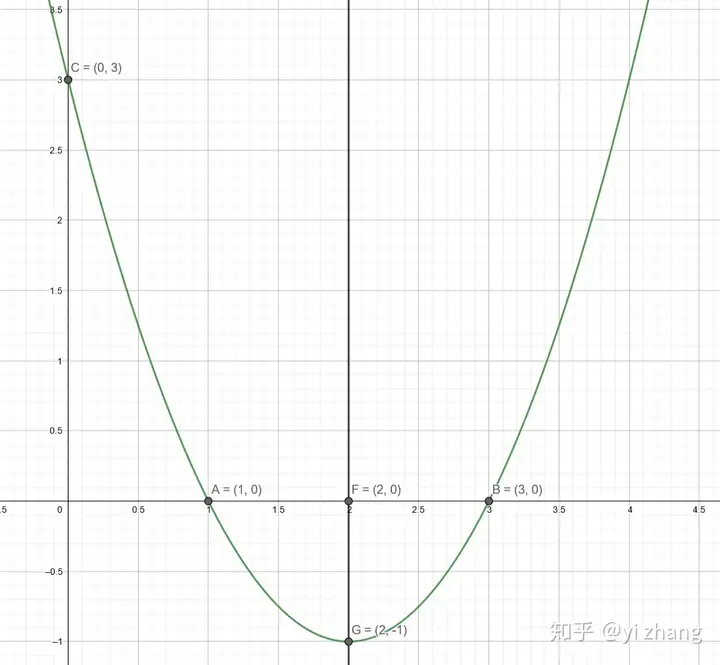
(实际函数为一般式: 或者写成顶点式: 两根式: )
我们先认为
那么可以得到几个点的坐标。
在此可以注意到,
2. b未出现,c是和y轴交点坐标属于一般式的。
3. h,k是属于顶点式的。(h,k)就是顶点坐标。
4. 是属于两根式的。分别是和x轴的两个交点。
但既然同一个二次函数可以用三种方式来表达。那么很显然,三者之间必定存在关系,以及能够相互转化。
(其实上面说法不准确,对于和x轴没有交点的无法采用两根式)
将一般式化成顶点式(这是任何情况下都成立的)
通过对比 可以发现
2. 一般式和两根式
由,
令y=0
就能得到一元二次方程的求根公式
按照前面的预设
那么
通过简单的加减就能得到
(其中1,3式就是韦达定理)
或者将 开括号
也能对比出
3. 顶点式和两根式
从上面的以及
可以看出,
当然也可以直观的从函数图形上得到。
二次函数的对称轴就是 连线的中点。
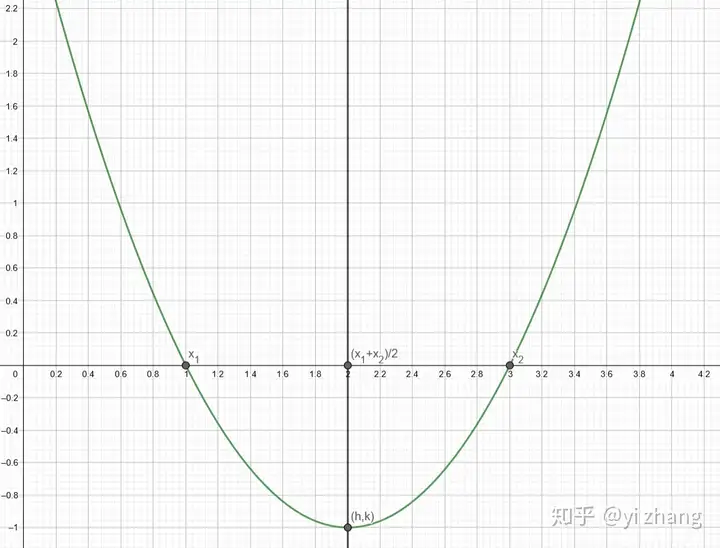
接下来对于顶点的纵坐标就并不那么直观了。
从代数上,我们观察下面两个式子。
能够发现
也就是k等于a/4*两根之间距离的平方的相反数。
我们也可以从几何上直观的看出来
还是以为例,
显然任意一个根到对称轴的距离为 ,因为抛物线任意平移形状不变。也就是我可以将任意抛物线平移后得到形如 ,例如 ,
横纵坐标保持着,纵坐标=1/2*横坐标的平方关系
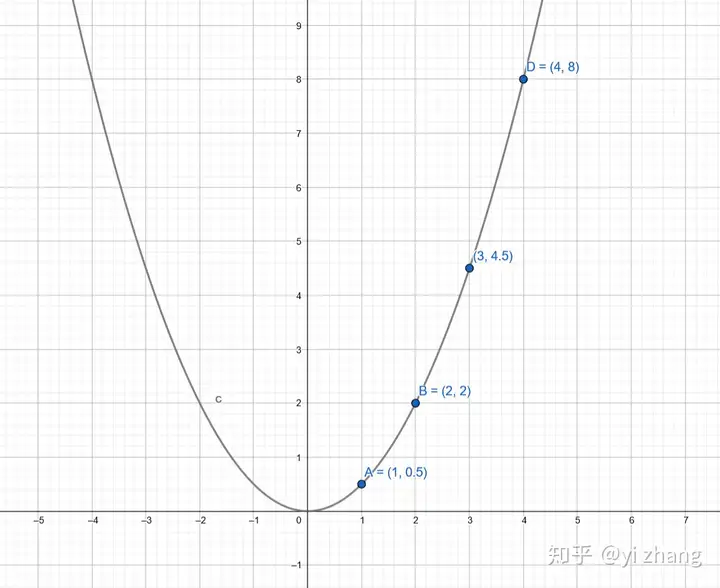
而其实这种平方关系存在于任意的抛物线,只要是对称轴上点就有的性质,即使和x轴没有交点,取一个尽可能大的数值,总能和抛物线相交两点。
我在对称轴上取一点H (对于这开口向上的抛物线,H点要在顶点上方)过H做直线平行x轴,交抛物线于D,E两点。
任意移动H点,可以发现
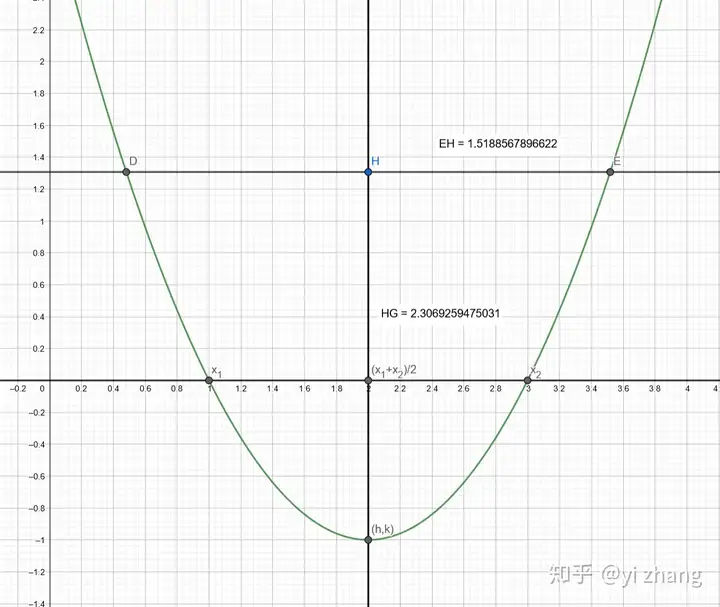
在来一个 的二次函数试下。
比如
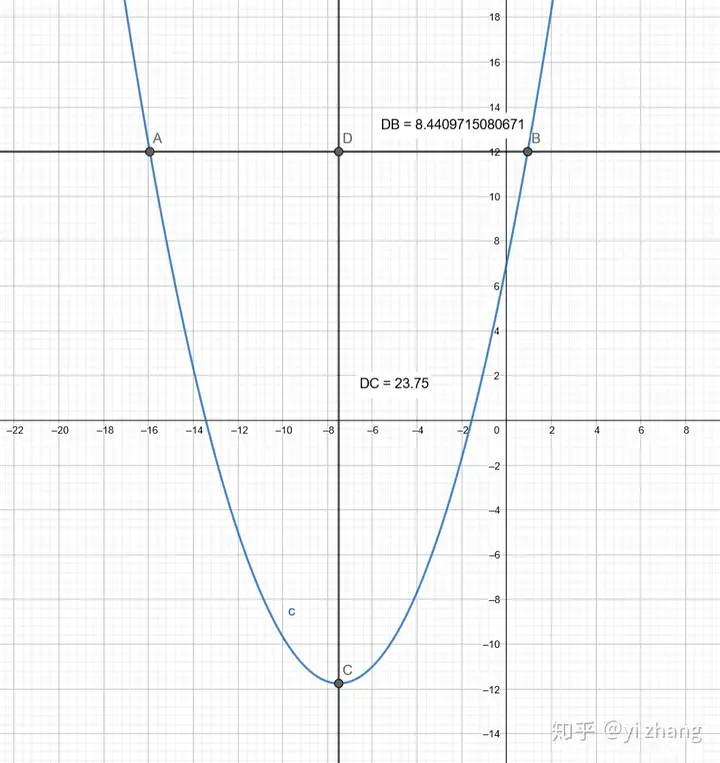
当BD=8.44时候,DC=23.75=8.44*8.44/3
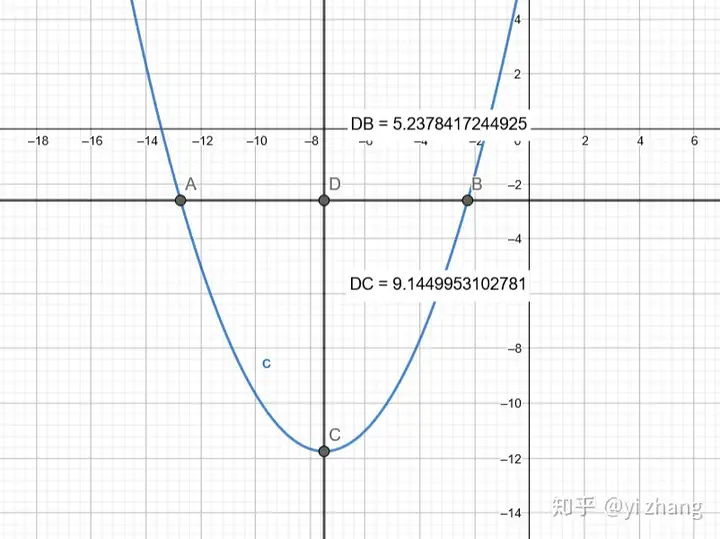
当BD=5.24时候,DC=9.14=5.24*5.24/3
上述总结,对于任意抛物线来说,抛物线上点的到对称轴的距离的平分*a=这个点和顶点之间的纵坐标之差。
欢迎使用手机、平板等移动设备访问中考网,2025中考一路陪伴同行!>>点击查看