来源:网络资源 2022-10-15 11:06:54
【例题】
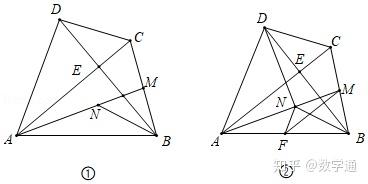
如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN
(1)求证:BN平分∠ABE;
(2)若BD=1,连接DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)若点F为AB的中点,连接FN、FM(如图②),求证:∠MFN=∠BDC.
【考查知识点】四边形综合题;几何综合题
【解题分析】
(1)由AB=AC知∠ABC=∠ACB,由等腰三角形三线合一知AM⊥BC,从而根据∠MAB+∠ABC=∠EBC+∠ACB知∠MAB=∠EBC,再由△MBN为等腰直角三角形知∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°就可以证明;
(2)设BM=CM=MN=a,知DN=BC=2a,证△ABN≌△DBN得AN=DN=2a,Rt△ABM中利用勾股定理可得a的值,从中得出答案;
(3)F是AB的中点知MF=AF=BF及∠FMN=∠MAB=∠CBD,再由MF/AB=MN/BC=1/2,即MF/BD=MN/BC,得△MFN∽△BDC,即可得证.
【详细解答】
(1)证明:如图①,∵AB=AC,
∴∠ABC=∠ACB,
∵M是BC的中点,
∴AM⊥BC,
在Rt△ABM中,∠MAB+∠ABC=90°,
在Rt△CBE中,∠EBC+∠ACB=90°,
∴∠MAB=∠EBC,
∵MB=MN,
∴△MBN是等腰直角三角形,
∴∠MNB=∠MBN=45°,
∵∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°,
∴∠NBE=∠ABN,即BN平分∠ABE;
(2)解:设BM=CM=MN=a,
∵四边形DNBC是平行四边形,
∴DN=BC=2a,
在△ABN和△DBN中,
∵AB=DB,角NBE=角ABN,BN=BN
∴△ABN≌△DBN(SAS),
∴AN=DN=2a,
在Rt△ABM中,由AM2+MB2=AB2,可得:(2a+a)2+a2=1,
解得:a=±根号10/10(负值舍去),
∴BC=2a=根号10/5;
(3)解:∵F是AB的中点,
∴在Rt△MAB中,MF=AF=BF,
∴∠MAB=∠FMN,
∵∠MAB=∠CBD,
∴∠FMN=∠CBD,
∵MF/AB=MN/BC=1/2,即MF/BD=MN/BC,
∴△MFN∽△BDC,
∴∠MFN=∠BDC.
【总结】
这道题属于四边形的综合题,解决这道题目的关键是掌握等腰三角形三线合一的性质、直角三角形和平行四边形的性质及全等三角形与相似三角形的判定与性质等知识点,如果掌握这些知识点,那么解决起来就不难了。
欢迎使用手机、平板等移动设备访问中考网,2025中考一路陪伴同行!>>点击查看