2023年初中数学反比例函数突破方法

我们先来看例题，最后会给大家总结反比例函数如何破题。

题目我们先易后难!

例题1：代表一类反比例函数定性分析题

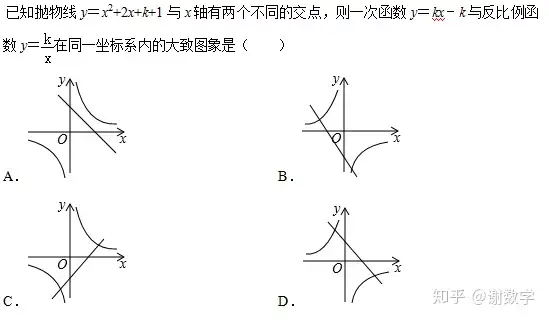
这类题目属于定性分析题，不要你实实在在算出具体数字的题目。但是要做对，也是需要你对反比例函数定义以及抛物线定义有所了解。这题不是单纯只考反比例函数内容还结合了抛物线知识。属于双线结合题。出题遵循先易后难，放在例题1，说明难度不大。抛物线有两个不同交点，说明▲=b²-4ac>0可以得到。计算出K<0反比例过二、四象限。直接排除A、C两个选项。接下来y=kx-k说明这个函数必过(1、0)点所以直接选D选项。如何理解必过(1.0)点，这个知识点经常考。y=kx-k=k(x-1) 当x取1时，无论K为何值。y必然为0 所以必过(1.0)点。

例题2：代表一类可求X与y分别是多少的反比例函数题

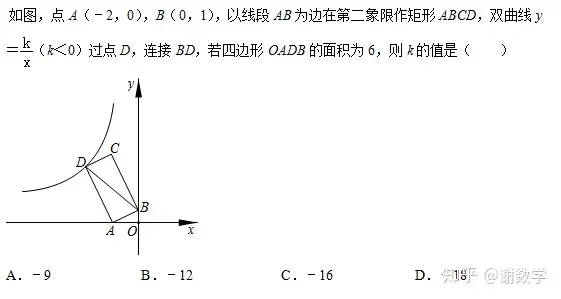
例题2难度不是很大。四边形OADB面积为6，四边形OADB是个不规则图形。那么不规则图形的面积计算方法必然是用割补法。很明显这个S图形OADB=S▲AOB+S▲ABD 因为S▲AOB=1则S▲ABD=5 2分之1的AB乘以AD等于5。接下来AB的长我们知道为 根号5 所以AD长为 2又根号5 当我们得到AD长以后。有什么作用呢?接下来就要说解反比例函数的思路了。反比例函数题大概率是求K值，求K值我们必然要联系到K=xy 这个代数式，那么要求K值必然要求xy相乘为多少。那么是不是分两种情况!!!

一种情况：我们可以单独求出X和Y各是多少。然后最后相乘求K

另外一种情况:题目无法求出X和Y各是多少，只能求出XY相乘的积是一个定值。那么积也是K

当你分清楚这两个问题后，再思考!要求X和Y其实质就是求线段的长度，那么是不是要做反比例函数上的点垂直X 轴和垂直Y轴的辅助线?所以出现反比例函数题目，不管你会不会做，先找反比例函数上的点做垂直X 轴和垂直Y轴的辅助线!!!

做完辅助线后必然的步骤就是求线段的长度了!!!那么求线段的长度也是我们经常遇到的数学题。求线段长度的方法有哪些呢?再我还没写出来的时候自己脑袋再思考思考。

想到了吗?

求线段长度经常用的方法有以下几种：

1、三角函数法：

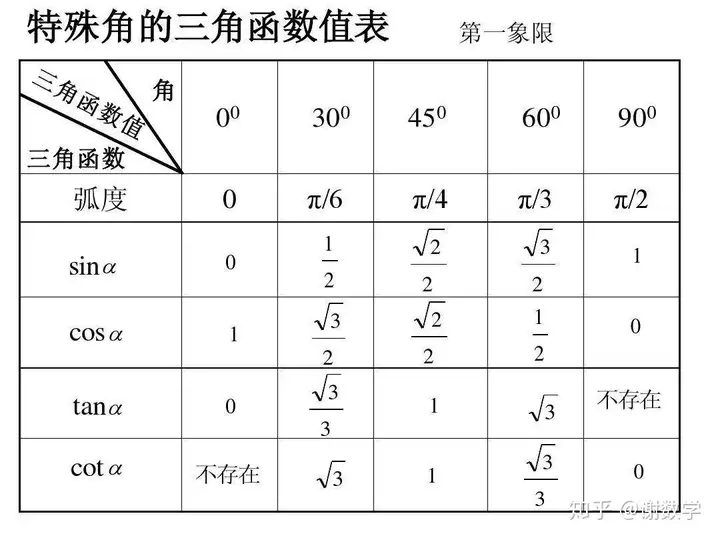
有涉及三角函数的必须是要在直角三角形里面去做。普通三角形给你其中一个内角是特殊角是没有任何意义的。因此要使用三角函数法求线段长度，也是需要在直角三角形里面找线段直接比例的。如果没有直角三角形，但是出现了上图的特殊角看看能不能构造直接三角形。

2、勾股定理：

这个方法始终贯穿我们初中阶段。

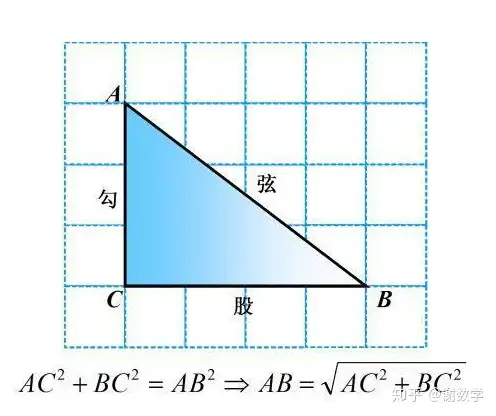
3、全等三角形的判定方法。(SSS/SAS/ASA/AAS/HL)五种判定全等三角形的方法记住了没有?

4、用证明相似三角形的方法求知线段的长度。

只要是用相似三角形的方法求线段长度，那么经常遇到如下模型：

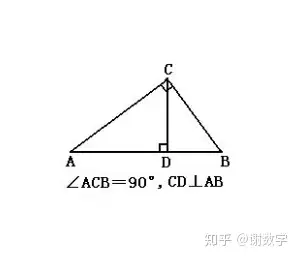
大直角三角形套小直角三角形模型简称大套小

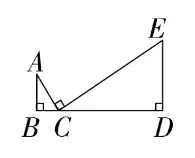
K模型

就是三个直角三角形两两相似的模型。

延伸了那么多题外知识点，我们回到刚才的题目。当你算出AD长为 2又根号5之后，所以你要想到做D点垂直X轴。然后得到了上面的K模型。

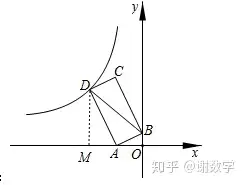
再用勾股定理求X=2因此 xy=16 记住经过二四象限K值为负数。最终答案为-16选C

例题3：代表一类含有2个反比例函数同时出现的题目

含有2个反比例函数的题目相对而言，会简单一定。这类题目考察的实质是。要会设点。

这个题目相对来说简单一点。

例题4：代表一类无法求X和Y各是多少的。可以求xy相乘是定值的题目

梯形OACB面积为4，梯形是规则图形，要把他们的面积表达式写出来的第一步。

第二步，不管会不会做，先做反比例函数上的点到X轴和Y轴的辅助线。

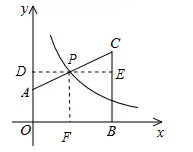
一步一步推理，答案就出来了。

例题5：代表一类反比例函数取值范围的题目

这类题目相对来说，你只要学一次，以后遇到都会做的类型。不比上面要思考好几个步骤，又要结合到全等，相似的题目，那么复杂。深刻理解有交点是什么意思。有没有交点几何意义其实就是平移反比例函数取只有一个交点时候就是临界点。那么很明显，A点就是最左边的临界点。因此K值必然最小值是2。那么最大值呢?其实就是反比例函数和线段BC只有一个交点的时候。

答案选A 这题你要学会把如何快速求K 的方法背下来。遇到这种知道平面直角坐标系上任意两点的可以迅速求出K值。

例题6：代表满足某种条件的定值面积的题型

这类题目看起来是很可怕的，但是实质这类题目当你学完我说的方法后，你会觉得太好用了。这类题目以后遇到再也不怕了!是不是觉得我说得神乎奇神?有点黄婆卖瓜，自卖自夸。步入正题。这类题目特征是什么?就是曲线上一个动点。看起来好可怕!反比例静止的定要求，我都怕。还来动点!不好意思，再下告辞。不!老乡别走。我take you fly

题目说P点是动点，实质就是无论P点如何运动，题目中要我们求的S▲POA必然是定值。那么图中有一个特殊点，就是P点运动到C2曲线和y 轴交点的位置时。是不是就可以运用到我们所学的万年勾股定理去求解了?有学生问，老师为什么要这样做?不好意思，如果不这样做。随便取任意一点求面积的话。华佗在世也解不了!(因为华佗是学医的，所以解不了)那么华罗庚会不会，我就不懂了。

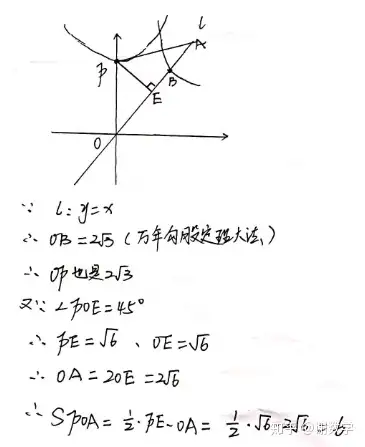
答案是：B

现在还觉得这类反比例函数动点可怕吗?记住方法找特殊点。千万别被出题老师思维带跑偏了。出题老师说动点，你真的去随便找一个点然后做辅助线。然后就没有然后了，根本没办法算。

例题7：代表反比例函数题中难度指数4颗星★★★★结合了多个知识点

首先我要告诉你的是，当题目中有看到中点字眼的题目，一定要想到三个常用关系式。

一是直角三角形，斜边上的中点。那么中线会等于斜边的一半。

二是想到如果题目中有A(x1.y1)和B(x2.y2)这两个点的坐标，那么AB线段的中点C横坐标为2分之x1+x2 ，C的纵坐标为2分之y1+y2

三是要想到三角形的中位线。

那么这个题目运用到的是哪个呢?很明显是第三个了。如何理解OQ最大值为2分之3是这个题目的解题关键。反比例函数是关于原点对称的点对称图形，所以只要是y=kx的函数必然会被反比例函数分成三段。其中AO=BO 是一定的。这个必须当做知识点背下来。Q又是AP的中点 。因此能得到OQ就是三角形APB的中位线。那么OQ取最大值，必然就是BP取最大值。然后根据题目意思可得。P点是圆上运动的动点，B是固定的点。要使得BP 最大，BP一定要过圆心C点。那么图就可如下图所画。

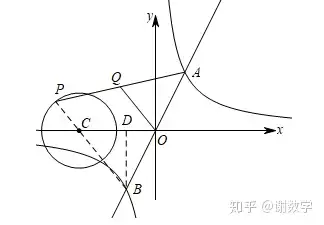
然后又回到刚才所说的，要求K，不管会做不会做，先找反比例函数上的点做垂直X轴和Y轴。那么这个题目中有两个点在反比例函数上。是A还是B?闭上眼睛也要选B?why

A点和B点谁的已知量更多?必然是B啦!(这就是解题思路)

又变成求线段长度的问题了。上面已经说了，求线段长度就那么4种常用的。这个题目用什么?勾股定理!why ?

因为整个题目做下来你是不是发现题目中还有一个已知条件没有用?一次函数y=2x

说到这里补充一个知识点，当你看y=x或者y=2x或者y=3x这样的一次函数。其实实质告诉你几何意义是这个函数和X轴构成的直角三角形的y/x比值是多少。然后可得到BD比OD在这个题目中等于2。接下来。设OD=X则BD=2X 则CD=2-X 又因为BP最大为3 所以BC为2 得到万年勾股大法：CD²+BD²=BC² 可解X=4/5 y=2x=8/5 K值=32/25 选C

例题8：这个题目代表一类知边长求面积比后解K值

我们看但C始终在双曲线上运动，是不是又是有点类似上面例题6，满足某种条件下。K值始终是一个定值。类似满足某种条件下，面积是个定值。有点神似!第一步。要干嘛?会做不会做，先把C垂直与x 轴和Y轴辅助线做了!!!!已经强调好几遍了，记到脑海里。

反比例函数和经过原点的kx=y又出现了。说明要想到AO=OB。题目中又有交代▲ABC为等腰三角形。又告诉你∠ACB=120°那么肯定要把OC连起来。自然而然的事情。因为120不属于上面所说的特殊角。60度才是特殊角度。

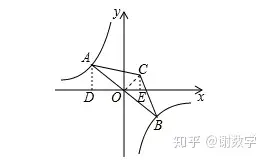
那么辅助线就是如图所示。如果你没有做出这个辅助线，一定要好好思考为什么自己的反比例函数解题思路没有形成。同时也希望看完我的思路能变成自己的。这次是你看这篇文章的用处。同时更希望学有所成，能将方法用到你接下来的中考里面。

做完辅助线我们发现，题目又回到上面我所说的K模型来了。出现了RT▲ADO RT▲AOC RT▲OEC 但是我们发现。整个题目是不是没有告诉你任何一边的长度?没有告诉我们任何一边的长度，那么我们要求K值，必然无法单个求X和单个Y值是多少。所以必然用第二种求K值的方法，就是求出xy相乘的值多少也可以做。

有三个RT▲相似，先把比例写出来。

相似三角形面积比等于边长比的平方

这当做定理背下来，对你解题非常有帮助。再补充个题外的。相似体的体积比等于边长比的3次方。

是不是有点不可思议的解题方法!叹为观止的感觉!

反比例函数题目很多，但是题型解题方法其实基本上就是上面几个类。当然反比例函数的难题也不仅仅是这几种。还有很多难度指数为5颗星★★★★★的题目，简单放个下面5颗星的题目给大家。大家有空可以尝试做一做。

这题答案为2

学完上面的方法，反比例函数题目。相信你们也不会看到就怕了。起码觉得有思路去破题。要学会总结平常自己遇到的题目。题目是海量的，题型其实是有限。考来考去，他们万变不离其宗。还有一个需要跟大家分享的：反比例函数如果出现整个题目只出现一个数字的!!!这类题实在不会做。你猜答案只能猜3个数字。

一是 : 数字本身。

二是：数字的2分之一。

三是：数字的2倍。

反比例函数大概率会附带图。具体数字是哪个?那么你要看图中给的数字线段的长度和要求的是什么结合起来。希望这个方法能在你实在想不出的时候帮你拿到分数。好比例题4.不会做!!!你猜也只能是4或者2梯形OACB面积为4。那么大的面积才为4 那么2的概率就更大了。这是解题技巧的问题。为什么会这样!!这是老师多年教学总结出来的经验之谈。

　　 欢迎使用手机、平板等移动设备访问中考网，2024中考一路陪伴同行！>>点击查看