来源:网络资源 2022-12-04 20:19:29
SSS的证明:
如果在两个三角形中,三条对应边相等(SSS),那么这两个三角形全等,其对应角相等。
已知:在△ABC和△DEF中,AB=DE,AC=DF,BC=EF
求证:△ABC≌△DEF
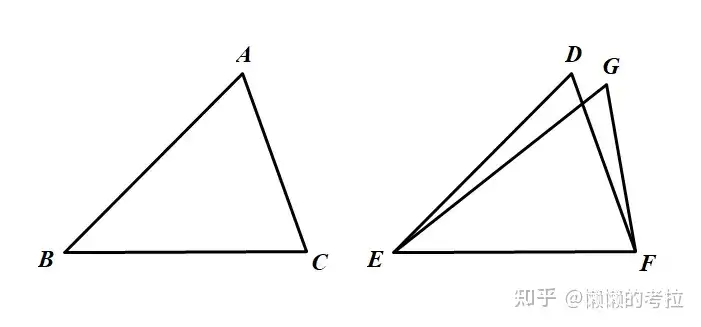
证明:
置点B于点E上,线段BC于直线EF上
∵BC=EF(已知)
∴点C与点F重合,即BC与EF重合
若△ABC≌△DEF不成立,则点A与点D不重合(公理4)
设点A对应点为点G,点G与点D不重合
连接EG,FG,有AB=GE,AC=GF
∵AB=DE,AC=DF(已知)
∴DE=GE,DF=GF(公理1.1)
∴在EF同侧,找到了点D与点G到EF相同端点的距离相等,这是不可能的。(命题1.7)
∴点G与点D重合
推导矛盾,故△ABC≌△DEF
二、SAS的证明:
如果两个三角形中两条对应边及其夹角相等(SAS),那么这两个三角形全等,其余对应角也相等。
已知:在△ABC和△DEF,AB=DE,AC=DF,∠BAC=∠EDF
求证:△ABC≌△DEF
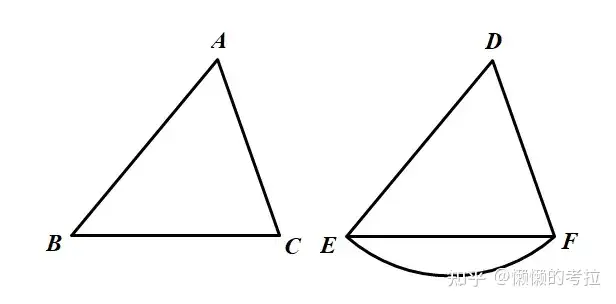
证明:
置点A与点D上,置AB于DE上
∵AB=DE(已知)
∴点B与点E重合
∵∠BAC=∠EDF(已知)
∴AC与DF重合
∵AC=DF(已知)
∴点C与点F重合
∴BC与EF重合 (公设1.1)
∴△ABC≌△DEF(公理1.4)
欢迎使用手机、平板等移动设备访问中考网,2025中考一路陪伴同行!>>点击查看