2023年初中数学：代数式及完全平方公式考点解析

考点：写代数式

代数式定义：由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子，或含有字母的数学表达式称为代数式。

例如：ax+2b，-2/3，b^2/26，√a+√2等。

注意

： 1、不包括等于号(=、≡)、不等号(≠、≤、≥、<、>、≮、≯)、约等号≈

2、可以有绝对值。

例如：|x|，|-2.25| 等

用运算符导(指加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子叫做代数式。数的一切运算规律也适用于代数式。单独的一个数或者一个字母也是代数

式，带有“<(≤)”“>(≥)”“=”“≠”等符号的不是代数式。

分类：在实数范围内,代数式分为有理式和无理式。

1）.有理式

有理式包括整式(除数中没有字母的有理式)和分式(除数中有字母且除数不为0的有理式)。这种代数式中对于字母只进行有限次加、减、乘、除和整数次乘方这些运算。

整式有包括单项式(数字或字母的乘积或单独的一个数字或字母)和多项式(若干个单项式的和)

1.单项式

没有加减运算的整式叫做单项式。

单项式的系数：单项式中的数字因数叫做单项式(或字母因数)的数字系数，简称系数

单项式的次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数

2.多项式

几个单项式的代数和叫做多项式;多项式中每个单项式叫做多项式的项。不含字母的项叫做常数项。

多项式的次数：多项式里，次数最高的项的次数，就是这个多项式的次数。

齐次多项式：各项次数相同的多项式叫做齐次多项式。不可约多项式：次数大于零的有理系数的多项式，不能分解为两个次数大于零的有理数系数多项式的乘积时，称为有理数范围内不可约多项式。

实数范围内不可约多项式是一次或某些二次多项式，复数范同内不可约多项式是一次多项式。对称多项式：在多元多项式中，如果任意两个元互相交换所得的结果都和原式相同，则称此多项式是关于这些元的对称多项式。同类项：多项式中含有相同的字母，并且相同字母的指数也分别相同的项叫做同类项。

2）.无理式

含有 字母的根式 或 字母的非整数次乘方的代数式叫做无理式。

书写格式：

(1)两字母相乘、数字与字母相乘、字母与括号相乘以及括号与括号相乘时，乘号都可以省略不写.如：“x与y的积”可以写成“xy”;“a与2的积”应写成“2a”，“m、n的和的2倍”应写成“2(m+n)”。

(2)字母与数字相乘或数字与括号相乘时，乘号可省略不写，但数字必须写在前面.例如“x×2”要写成”2x”，不能写成“x2”;“长、宽分别为a、b的长方形的周长”要写成“2(a+b)”，不能写成“(a+b)2”。

(3)代数式中不能出现除号，相除关系要写成分数的形式

(4)数字与数字相乘时，乘号(也可以写作 · )仍应保留不能省略，或直接计算出结果.例如“3×7xy”不能写成“37xy”，最好写成“21xy”。

练习&解析

现有大小两艘轮船，小船每天运 x吨货物，大船比小船每天多运10吨货物.现在让大船完成运送100吨货物的任务，小船完成运送80吨货物的任务。

(1)分别写出大船、小船完成任务用的时间?

(2)试说明哪艘轮船完成任务用的时间少?

解：(1)大船完成任务的时间为：

;

小船完成任务的时间为：

;

(2)

﹣

=

=

，

x>40时，小船所用时间少;

x=40时，两船所用时间相同;x<40时，大船所用时间少.

考点：完全平方公式

完全平方公式是进行代数运算与变形的重要知识基础。该知识点重点是对完全平方公式的熟记及应用，难点是对公式特征的理解 (如对公式中积的一次项系数的理解)。

两数和(或差)的平方，等于它们的平方和，加上(或减去)它们的积的2倍，叫做完全平方公式。为了区别，我们把前者叫做两数和的完全平方公式，后者叫做两数差的完全平方公式。

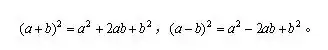
理解公式左右边特征

(一)学会推导公式(这两个公式是根据乘方的意义与多项式的乘法法则得到的)，真实体会随意“创造”的不正确性;

(二)学会用文字概述公式的含义：两数和(或差)的平方，等于它们的平方和，加上(或减去)它们的积的2倍.

都叫做完全平方公式.为了区别，我们把前者叫做两数和的完全平方公式，后者叫做两数差的完全平方公式.

(三)这两个公式的结构特征是：

1、

左边是两个相同的二项式相乘，右边是三项式，是左边二项式中两项的平方和，加上或减去这两项乘积的2倍;

2、

左边两项符号相同时，右边各项全用“+”号连接;左边两项符号相反时，右边平方项用“+”号连接后再“-”两项乘积的2倍(注：这里说项时未包括其符号在内);

3、

公式中的字母可以表示具体的数(正数或负数)，也可以表示单项式或多项式等数学式.

(四)两个公式的统一：因为

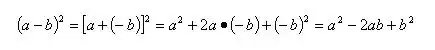
所以两个公式实际上可以看成一个公式：两数和的完全平方公式。这样可以既可以防止公式的混淆又杜绝了运算符号的出错。

练习&解析

完全平方公式的基本变形：

(一)变符号

例：运用完全平方公式计算：

(1)(-4x+3y)²

(2)(-a-b)²

分析：本例改变了公式中a、b的符号，以第二小题为例，处理该问题最简单的方法是将这个式子解答：

(1)16x²-24xy+9y²

(2)a²+2ab+b²

(二)变项数：

例：计算：(3a+2b+c)²

分析：完全平方公式的左边是两个相同的二项式相乘，而本例中出现了三项，故应考虑将其中两项结合运用整体思想看成一项，从而化解矛盾。所以在运用公式时，(3a+2b+c)²可先变形为[(3a+2b)+c]²，直接套用公式计算。

解答：9a²+12ab+6ac+4b²+4bc+c²

(三)变结构：

例：运用公式计算：

(1)(x+y)(2x+2y)

(2)(a+b)(-a-b)

(3)(a-b)(b-a)

分析:本例中所给的均是二项式乘以二项式，表面看外观结构不符合公式特征，但仔细观察易发现，只要将其中一个因式作适当变形就可以了，即

(1)(x+y)(2x+2y)=2(x+y)²

(2) (a+b)(-a-b)=-(a+b)²

(3) (a-b)(b-a)=-(a-b)

　　 欢迎使用手机、平板等移动设备访问中考网，2025中考一路陪伴同行！>>点击查看