2023年初中数学平面几何压轴题6大模型及解题方法

全等模型之三垂直、三等角模型

三垂直、三等角模型

定义：三个等角的顶点在同一条直线上构成的图形，这个角可以是直角，也可以是锐角或钝角，一般是以等腰三角形或者等边三角形为背景。这个模型贯穿初中几何的始终，初三讲《相似三角形》时这也是一个非常重要的知识点

方法提炼

1 若题目中有一线三(直角)等角，可以直接证明相似或全等实现边与角的转化;

2 若题目中没有给出一线三(直角)等角，可以根据需要来构造

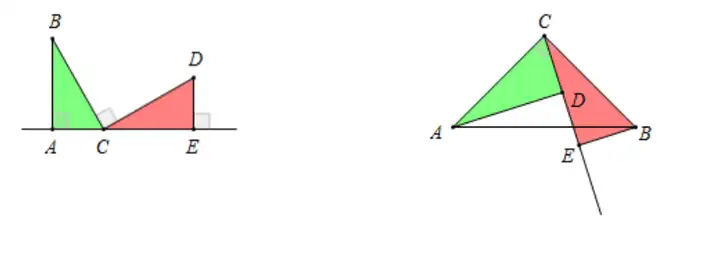
基本模型：(1)一线三垂直

【基本图形】

全等模型之半角模型

定义：夹半角，顾名思义，是一个大角夹着一个大小只有其一半的角，如下图所示。

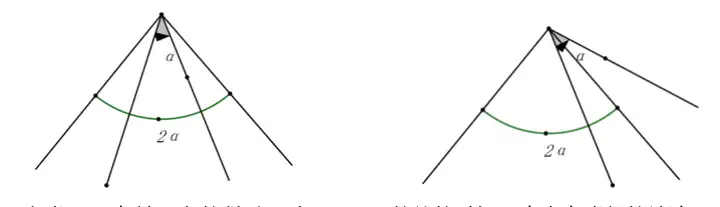
这类题目有其固定的做法，当a取不同的值的时候，也会有类似的结论

夹半角的常见分类：

(1)90 度夹 45 度

(2)120 度夹 60 度

(3)2α夹α

题型一 90 度夹 45 度

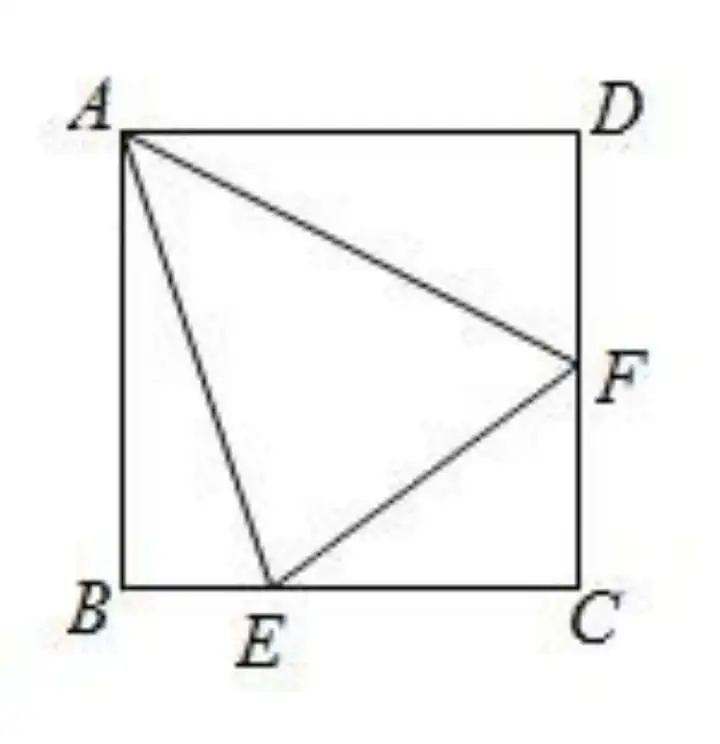
【例 1】 如图，正方形ABCD 中，E在BC上，F在CD上，且∠EAF=45°，求证：(1)BE+DF=EF

(2)∠AEB=∠AEF

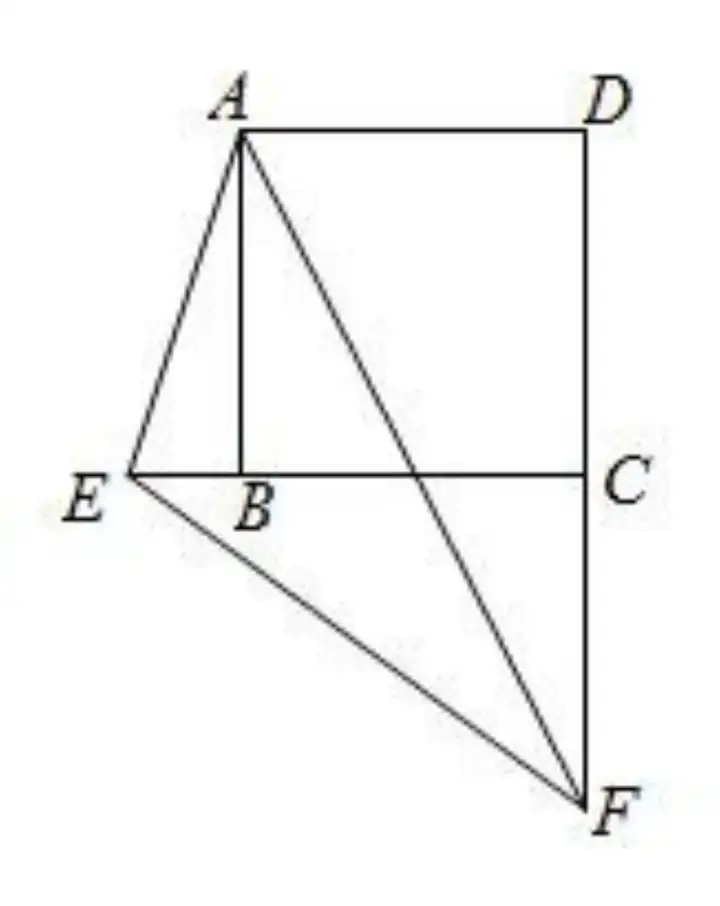
(2)在例 1 的条件下，若E在CB延长线上，F在DC延长线上，其余条件不变，证明：

(1)DF-BE=EF

(2)∠AEB+∠AEF=180°

中点模型

模型1.倍长中线或类中线(与中点有关的线段)构造全等三角形

如图①，AD是△ABC的中线，延长AD至点E使DE=AD，易证：△ADC≌EDB(SAS)。

如图②，D是BC中点，延长FD至点E使DE=FD，易证：△FDB≌△EDC(SAS)。

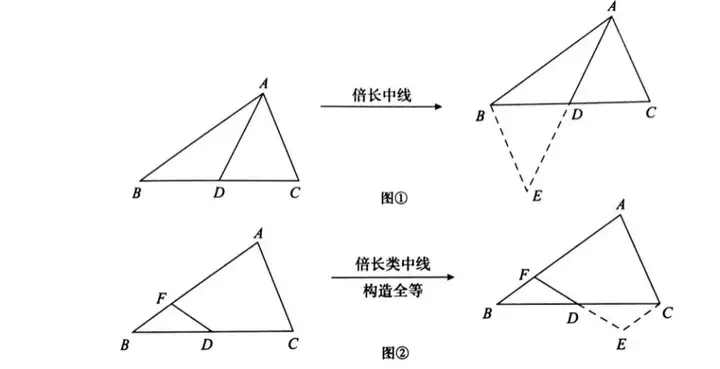
模型分析：

当遇见中线或者中点的时候，可以尝试倍长中线或倍长类中线，构造全等三角形，目的是对已知条件中的线段进行转移。

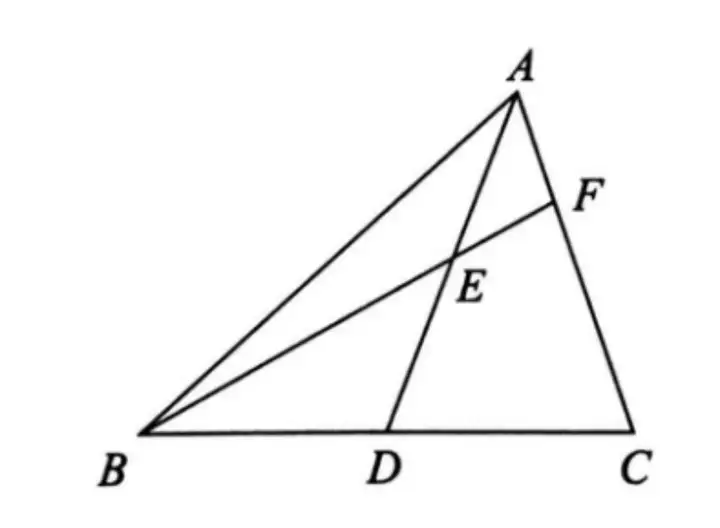
例1. 如图，已知在△ABC中，AD是BC边上的中线，E是AD上一点，连接BE并延长交AC于点F，AF=EF。求证：AC=BE。

模型2.已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”

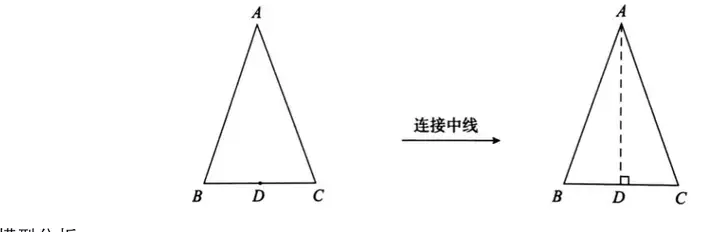
模型分析：

等腰三角形有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等或边相等。为解题创造更多的条件，当看到等腰三角形的时候，就应想到“边等、角等、三线合一”。

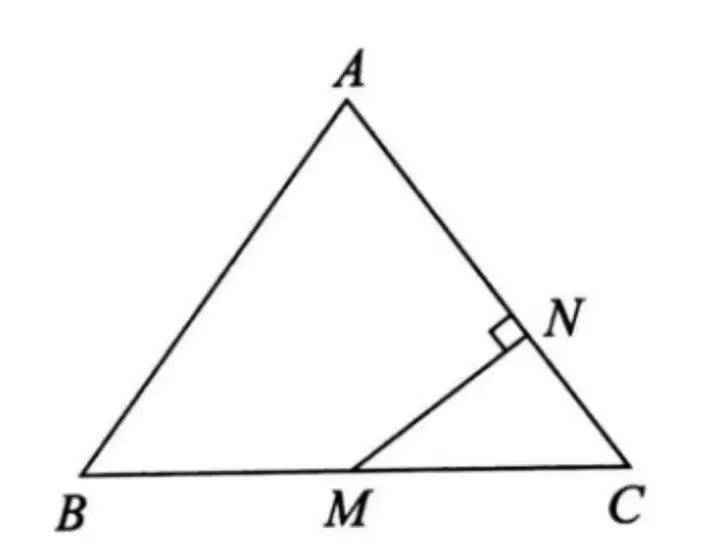
例.如图，在△ABC中，AB=AC=5，BC=6，M为BC的中点，MN⊥AC于点N，求MN的长度。

模型3.已知三角形一边的中点，可以考虑中位线定理

模型分析：

在三角形中，如果有中点，可构造三角形的中位线，利用三角形中位线的性质定理：DE∥BC，且DE=1/2BC来解题。中位线定理中既有线段之间的位置关系又有数量关系，该模型可以解决角相等，线段之间的倍半、相等及平行问题。

例. 在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，分别与BA、CD的延长线交于点M、N。求证：∠BME=∠CNE。

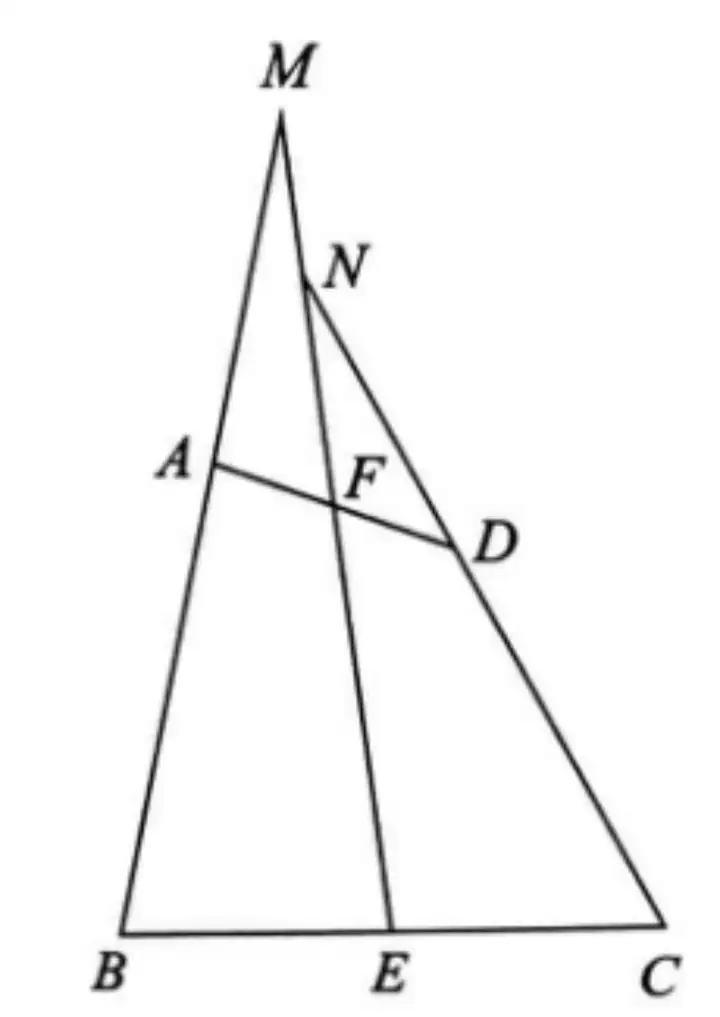
模型4.已知直角三角形斜边中点，可以考虑构造斜边中线

模型分析：

在直角三角形中，当遇见斜边中点时，经常会作斜边上的中线，利用直角三角形斜边上的中线等于斜边的一半，即CD=1/2AB，来证明线段间的数量关系，而且可以得到两个等腰三角形：△ACD和△BCD，该模型经常会与中位线定理一起综合应用。

例. 如图，在△ABC中，BE、CF分别为AC、AB上的高，D为BC的中点，DM⊥EF于点M。求证：FM=EM。

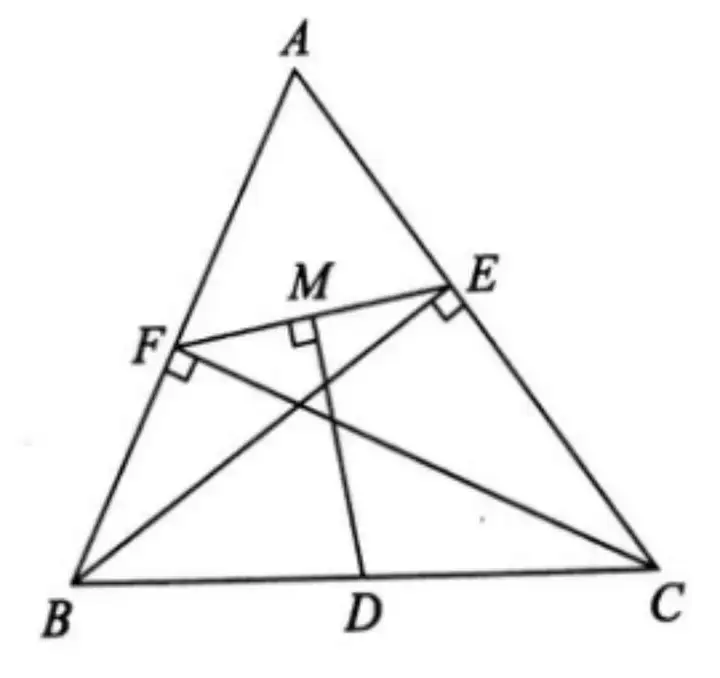
手拉手模型

例1、在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，证明：

(1) △ABE≌△DBC

(2) AE=DC

(3) AE与DC的夹角为60。

(4) △AGB≌△DFB

(5) △EGB≌△CFB

(6) BH平分∠AHC

(7) GF∥AC

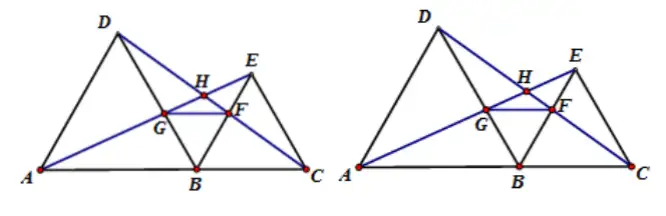
变式练习1、如果两个等边三角形△ABD和△BCE，连接AE与CD，证明：

(1) △ABE≌△DBC

(2) AE=DC

(3) AE与DC的夹角为60。

(4) AE与DC的交点设为H,BH平分∠AHC

奔驰模型

截长补短

截长补短法构造全等三角形

截长补短法，是初中数学几何题中一种辅助线的添加方法，也是把几何题化难为易的一种思想.所谓“截长”，就是将三者中最长的那条线段一分为二，使其中的一条线段等于已知的两条较短线段中的一条，然后证明其中的另一段与已知的另一条线段相等;所谓“补短”，就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等，然后求出延长后的线段与最长的已知线段的关系.有的是采取截长补短后，使之构成某种特定的三角形进行求解.

截长补短法作辅助线，适合于证明线段的和、差、倍、分等类的题目.

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看