2023年初中数学如何学习初中函数（一次函数篇）

复习

复习是个好习惯，在进行本篇内容之前我们先回忆上一篇内容得出的结论：(还指望我粘贴复制吗，当然要你背啦)

复习完毕，开始正题

1.解析式的由来

上一篇的内容，帮我们建立了几何观念上的函数即：函数是线。只有几何观念，对于函数来讲是完全不够的，属于缺胳膊少腿，不完整。数学数学，没有代数就没有灵魂，所以今天我们来把它的灵魂给它装进去。毕竟是要装灵魂嘛，是个技术活，那就先拿最简单的练练手，也就是一次函数，看看它的躯壳

噫，花里胡哨，乱七八糟。先拿一个出来，用放大镜看一下

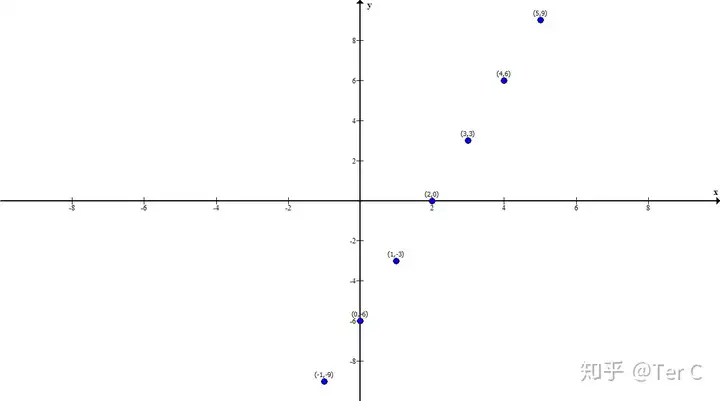
嗯，有那么点儿意思了，原来函数线真的是由坐标点组成的，我们上一篇的理论就被实锤了。这点被实锤了，那是不是就可以这样理解函数的代数化=坐标点的代数化。而且，非常巧的是，每一个坐标点都有着相对应的横坐标和纵坐标来表达其身份地位，横坐标、纵坐标又刚好是数字。苹果都砸到你头上了，下一步该怎么办不用我多说了吧，当然是把它们列出来好好观察啊。

(5，9)(4，6)(3，3)(2，0)(1，-3)(0，-6)(-1，-9)

观察完毕后，按照牛顿的做法，你是不是就想问：为什么这些点在一条直线上?然后我就想一粉笔头砸你头上，忘了前一篇的内容了?因为它们有规律啊!!!既然是规律，那就是变化，是变化按照我们的通用解法，先来个后面的减前面的。这里是坐标点，所以我们就后面的横坐标减前面的横坐标，纵坐标同理。

先来横坐标

4-5=-1

3-4=-1

2-3=-1

1-2=-1

可知都等于-1

再来纵坐标

6-9=-3

3-6=-3

0-3=-3

-3-0=-3

可知都等于-3

看出道道了嘛，反正我看出来了，那就是在相邻坐标点之间，横坐标减1，纵坐标要减3，反过来横坐标加1，纵坐标要加3。这到底对不对呢，不妨做一下验证，按照这个思路，分别找出(5，9)前面的坐标点和(-1，-9)后面的坐标点。(5，9)前面坐标点的横坐标为6，从5到6横坐标加1，那纵坐标加3即点(6，9)同理可得(-1，-9)后面的坐标点为(-2，-12)，描点连线

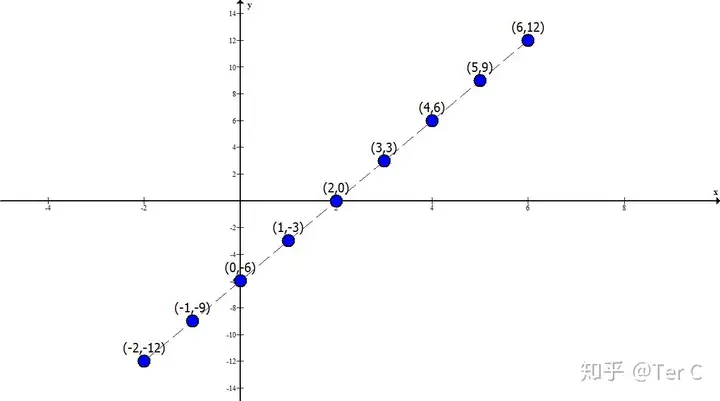
很明显，新得出的点和原来的点是在一条直线上，证明我们得到的规律是没有错的。既然相邻坐标点之间，有着横坐标减1，纵坐标要减3，反过来横坐标加1，纵坐标要加3这样的规律，是不是就万事大吉了呢?显然不是，比如，请你找出(-2，-12)之后的第50个坐标点。那你岂不是要重复上面的做法50遍?50遍你说你行，好，那请问第2020个呢?你还说你行，我再问第20102949203个呢?不行了吧。too young too simple。这就说明我们得到的规律不够普遍，不足以用于计算，需要继续推广化。

我们在小学二年级学过加减法的推广运算是乘除法，我们就把规律总结为乘除的规律即纵坐标的增加量是横坐标增加量的3倍。先验证一下符不符合原来的比如(5，9)和(2，0)用一下新得到的规律

从5到2增加了-3，纵坐标就要增加-9，9+(-9)=0，bingo正确。

后的第50个坐标点再计算(-2，-12)之后的第50个坐标点

在-2后面，又是第50个，所以横坐标=-52，根据规律有纵坐标=-12-50*3=-162

同理可计算任意坐标点

观察计算过程可知，计算本条直线的任意坐标点，需要用到我们的规律和一个已知坐标点。

满足于本条直线坐标点的规律找到了，别忘了我们的最终目标：规律代数化。我们任意给出本条直线上一坐标点(x，y)，选取(5，9)为基准坐标点。

纵坐标的增加量

y-9

横坐标的增加量

x-5

纵坐标的增加量是横坐标增加量的3倍

y-9=3*(x-5)

得y=3x-6

所以y=3x-6代表了本条线的所有坐标点，进而代表了本条直线

还没完，这条线是3倍，那有没有4倍，5倍，6倍，肯定是有的，所以我们就令k=任意常数，顺理成章的就把这个规律推广到了所有一次函数线即在一次函数线中，纵坐标的增加量是横坐标增加量的k倍。现在要完成这条规律代数化，以表达所有的一次函数线。已知一条一次函数线，纵坐标的增加量是横坐标增加量的k倍，已知坐标点(m，n)，求任意坐标点(x，y)。

纵坐标的增加量

y-n

横坐标的增加量

x-m

纵坐标的增加量是横坐标增加量的k倍

y-n=k*(x-m)

y=kx+n-km(看起来太复杂不清爽)

不妨令b=n-km

所以y=kx+b

大功告成y=kx+b就是所有一次函数线的代表

做了这么多的工作，终于把一次函数从直线变成了y=kx+b这样一条代数式，又是求解又是分析的，给这条代数式起个名字吧就叫解析式。几何方面的一次函数都有定义，代数方面的自然不能少，结合以上内容就是一次函数的定义形如y=kx+b(k，b为常数，k≠0)，其中x为自变量y为因变量，叫做一次函数

老规矩总结一下

perfect，接下来看性质

2.相关性质

说到性质，必然就是考察的重点，也就是痛点了，怎么才能把性质记好?喂，这是数学欸，当然是要理解记忆最好了啊。那我要理解谁呢?喂，解析式都给你了，你看啊，y=kx+b，当然是理解k和b怎么影响函数了啊

k值怎么影响函数

从定义里我们知道k=任意常数，我们在小学二年级学过数是有大小有正负的，就从这两个方面来看k值对于一次函数线的影响。

(1)正负

在研究k值，根据控制变量法，需保持b值不变，干脆一点直接让b=0。列几个k值正负不同的解析式，然后作图观察

y=2x | y=4x | y=12x | y=-2x | y=-8x | y=-12x

作图流程：求点坐标、描点、连线

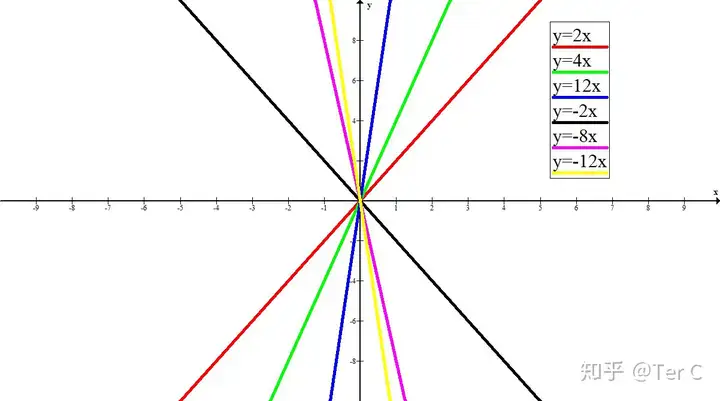
看图很容易发现

k>0的一次函数，图像都经过第一、第三象限

k<0的一次函数，图像都经过第二、第四象限

由此可知k值的正负影响着一次函数坐标点的分布

k的正负不同y随x的变化情况也不同

(2)大小

研究方法同上，还是它们几个

y=2x | y=4x | y=12x | y=-2x | y=-8x | y=-12x

作图流程：求点坐标、描点、连线

可以看到红、绿、蓝三条线的k值分别为2、4、12，很容易发现

当k>0时

k值越大，图像与x轴夹角就越大

图像与x轴夹角永远都是锐角

当k<0时

k值越大，图像与x轴夹角也是越大

图像与x轴夹角永远都是钝角

因此k值有个额外称呼叫：斜率

b值怎么影响函数

跟k值的研究方法意义，但是我们不能让k=0，因为定义不允许，因此我们保持k值不变。列几个k值相同b值不同的大家观察一下就好了。

y=2x+1 | y=2x+3 | y=2x+5 | y=2x-1 | y=2x-3 | y=2x-5

作图

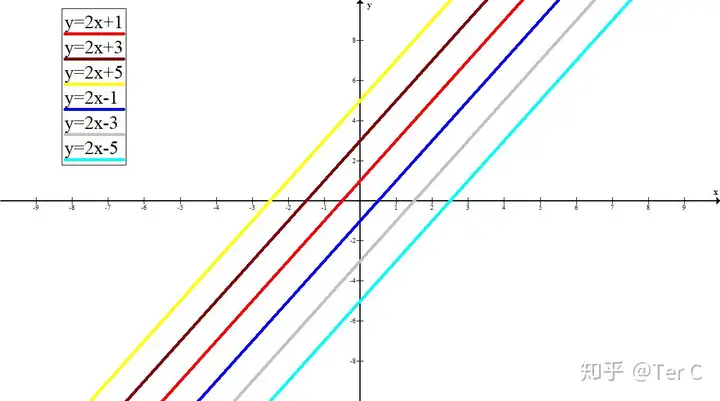
也非常明显

b>0时

图像与y轴交于y轴正半轴

b值越大，与y轴交点越靠上

b<0时

图像与y轴交于y轴负半轴

b值越小，与y轴交点越靠下

还可以发现

k值相同，直线都是平行的

这些直线都可以用y=2x向上或向下平移相应个单位得到

b值也有个额外称呼叫：截距

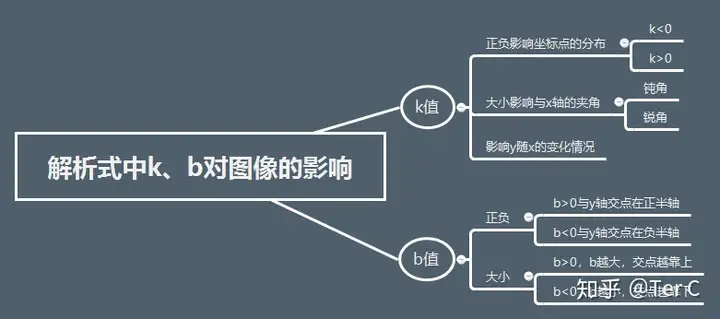
小段总结

3.相关考点

(1)图像考察

#1给图像辨别k值、b值正负与大小(经常与其它函数结合)

#2给b值、k值辨别图像

#3图像实际应用(k>0，第一象限内)

原理：x值相同，k值越大，y值越大

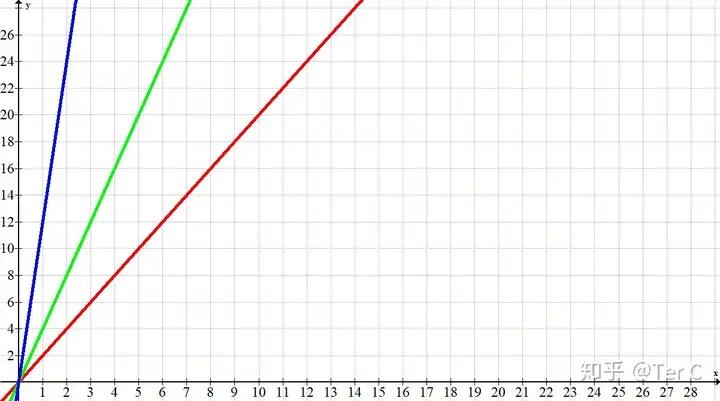
#4如图所示，当x=5时，y值大小依次是：红线<绿线<蓝线

##考察方式为，把横纵坐标U/I即为初三物理电学图像考察，换成m/v即为初二物理质量与密度图像考察，换成F/V即为初二浮力图像考察，同理还有v-t图、s-t图等等，贯穿初高中物理，高中物理还可以用图像解决复杂匀加匀减的位移问题

#5化学也同理可换

#6学数学的同时，把这么多的理化问题都学了，我就问你爱了没有。真是捡到宝了呢，哈哈哈哈哈

(2)求解析式

#1这个题目的原理就是两点确定一条直线

知道任意两点坐标，代入y=kx+b，可得关于k、b的二元一次方程，解出k、b就可以了，不多说。不会就去学一下二年级学过的解二元一次方程

#2你也可以先求k，再用我教你的计算方法，不过还是推荐课本的解法，还能练习一下解二元一次方程

(3)解应用题

#1关键在于设未知数，列方程，复杂一点的可能要结合图像，考察“数形结合”这个数学思想

#2动点问题里如果关系式为一次函数关系，要结合取值范围来求解

(4)与其它函数组成综合问题

#1求面积

#2求长度

#3求相应的最大最小值，要结合取值范围来看

#4求坐标点

(5)函数与方程

#1只需要理解一点，当y=0时，一次函数就变成了kx+b=0，也就变成了一元一次方程。

#2从代数层面看坐标点(x，0)的横坐标是对应方程的解

#3从几何层面看一次函数图像与x轴交点为一个方程点，理解好这里对于二次函数根的理解很有帮助

(6)函数与不等式

#1这里还是“数形结合”思想的应用

#2比如2x+1>0，可以看出y=2x+1这个函数的y>0，也就是x轴上方的图像

#3如2x+1>-3x+4，可以看成y1=2x+1与y2=-3x+4这两个函数图像的比较

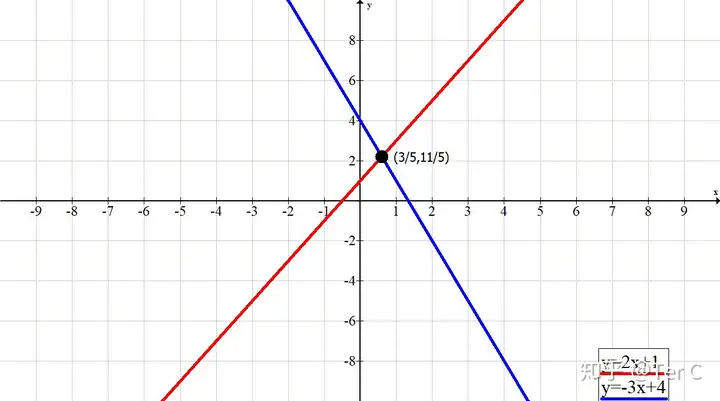
##第一步要找到交点，看图可知交点坐标为(3/5，11/5)

##没有交点就是没有解

##第二步要分两部分看，交点左边和交点右边

##该图可知交点左边，蓝线骑在红线头上，所以是2x+1<-3x+4对应不等式的解为x<3/5

##交点右边是红线骑在蓝线头上，所以是2x+1>-3x+4对应不等式的解为x>3/5

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看