2023年初中数学一元二次方程高级解题思路

第一讲，我们从一元二次方程开始。

中考中，方程的考核有几个：一元一次、二元一次、一元二次、分式方程、不等式，这其中，最难的也是必考的就是二元一次方程，也是和后续二次函数结合最紧密的考点，所以，今天我们先讲。

首先，我们来看一下，初中关于方程和不等式，都学了哪些知识点?下面这些图，就是这部分知识点的思维导图。

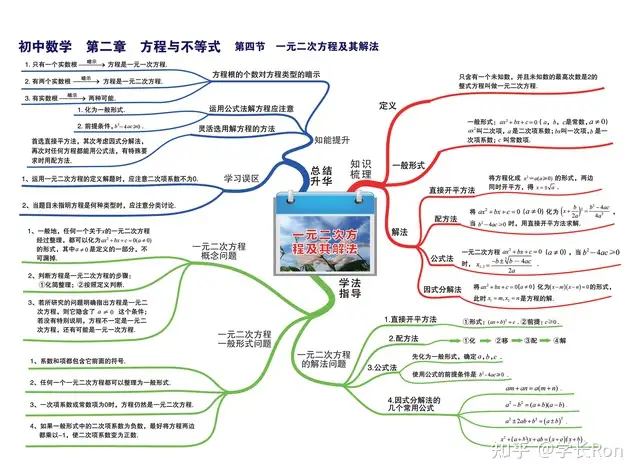
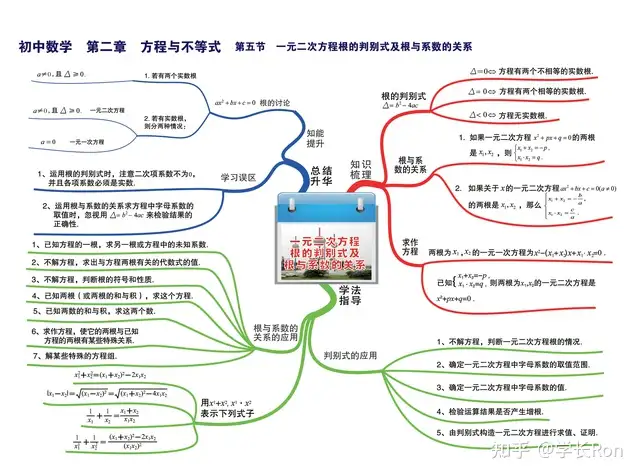
上面两张图，包括了初中阶段，一元二次方程、不等式的所有知识点，如果同学和孩子还有不知道的点，一定要从书本开始，把基础的部分打扎实。

第二，我们来讲一下一元二次方程在考试中，一般会怎么考?我们该用什么方法来应对。

什么是一元二次方程?

我们把形如

的方程叫一元二次方程。常见的解题方法有以下几种：配方法、公式法、因式分解法。其中，公式法是解一元二次方程的最普遍、最具有一般性的方法。

为什么说公式法是最普遍，也最具有一般性?

一元二次方程中，常见的判别式“

”，求根公式，包含了初中阶段所有学过的代数运算(有分式、有根运算、有幂运算)。同时，它也回答了，求解一元二次方程的诸多问题，比如：怎样求实根、实根的个数、何时有实根等基本问题……这也是，中考中，常见的几个考点。

除了上面说的，三种解题方法，还有什么更好用的方法呐?

显然是有的，告诉大家，解一元二次方程，最基本、最核心的思路就是：降次转化。

为什么这么说?因为，有些题目中的条件，用公式法运算量很大，甚至在解题过程中，会出现不合理的结果。所以，我们就要想办法去做一些变形、代换的处理。常用到的降次转化的方法有：变形降次、整体代入、构造零值多项式等。

下面给大家举几个例子：

思路指点：

首先，我们要弄明白基础概念，什么情况下会等于1?其次，根据不同的情况，求得结果。最后，带入验算，和定理、定义对照，是不是符合?

思路指点：

常用的方法，解出这两个根，发现要用公式法，计算非常繁琐。那么我们该怎么简化?这个时候，我们就要想到，降次转化的基本思路。提示一下，

，同样，，降次以后，我们的计算是不是变得很简单。

思路指点：

首先，题目给大家设置了陷阱——“关于x的方程”，没有说一次，还是二次，你发现了没?其次，发现了这个陷阱，就会变得简单，分情况计算，就可以了。

思路指点：

这道题，和上一题一样，设置了一个陷阱——绝对值。那么，我们就要讨论，这个绝对值里面的值是大于等于0，还是小于0?分情况计算，在结合绝对值里面的值是大于等于0，还是小于0，验算就行了。最后，我们来一个有点难度的。

思路指点：

看上去，这道题很复杂，其实，都是用来干扰你的。出题人，就是要你觉得很复杂，产生一种危难的情绪，然后，放弃掉。

其实，里面是四个等式，然后一个未知数x，其余的啊a,b,c,d，都是常数。我们在解题的时候，就很简单了，把a,b,c,d，四个常数，用一个来表达替换，比如：b,c,d都用a来表示，就会立马简化很多。

最后，我们来总结一下，一元二次方程的变形，主要就是下面的几种方式。另外，在没有说明是几次方程的时候，有绝对值的时候，需要分情况讨论、计算。

作业布置：

　　 欢迎使用手机、平板等移动设备访问中考网，2024中考一路陪伴同行！>>点击查看