2023年初中数学反比例函数知识点和题型总结大全

反比例函数在初中数学的函数学习中，占据着较为重要的位置。下面我们来梳理一下有关反比例函数的知识:

反比例函数的基本内容

定义:

如果两个变量x，y之间的对应关系可以表示成y=k/x(k为常数，k≠0)的形式，那么称y是x的反比例函数。函数表达式为：

◆ y=k/x

◆ y=kxˉ1

◆ xy=k

注意：反比例函数成立的条件是：k为常数且k≠0。该条件同时成立，同学在解题过程中往往容易忽视其成立条件，从而在取值范围的确定中易出错。

函数的增减性:

当k>0时，图象分别位于第一、三象限，同一个象限内，y随x的增大而减小;

当k<0时，图象分别位于二、四象限，同一个象限内,y随x的增大而增大。

性质：

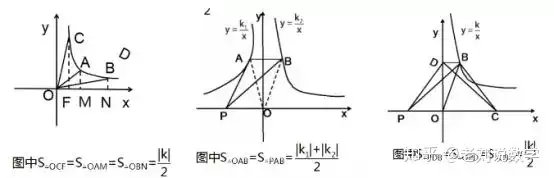
(1)反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2;

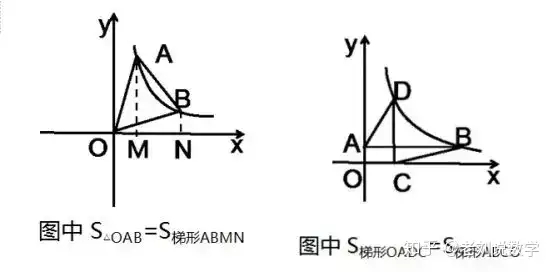
(2)图像上任意两点与原点构成的三角形的面积等于直角梯形的面积;

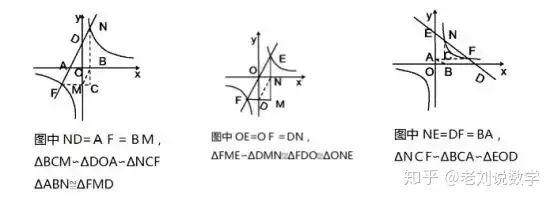
(3)反比例函数与一次函数相交时，存在线段相等的关系，坐标点关于原点对称的关系;

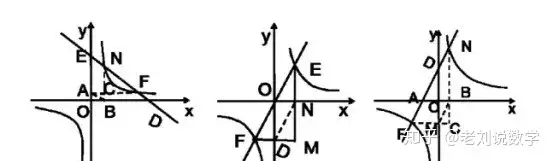
(4)反比例与一次函数有交点时，可以联立求出交点坐标(二次联立可以求一元二次方程，反映方程根的个数问题)。

反比例函数常考题型

结合近几年的考情分析，反比例函数往往出现在填空题和解答题中，其出题类型一般与一次函数、三角函数、相似、全等、圆等相结合，成为学生的“一大障碍”，但是其单独出题时，相对简单。

判断函数图像

① 看系数：一次函数只有一个未知数a;

注意：若一次函数的一次项系数与反比例函数的反比例系数正负相同，直线与双曲的两支都有交点。

② 找矛盾：通常需要运用排除法，排除错误选项得到正确答案。反比例函数只有一个未知数，因此常从反比例函数的图象入手进行判断。如果a>0，反比例函数图像在第一、三象限，如果a<0，反比例函数图象在第二、四象限。

注意：当反比例函数与其他函数相结合出题时，需要再判断其他函数图象经过的象限就可确定其函数图像。

求解析式一般需要求出函数图象上的点的坐标，函数解析式上有几个未知数，就要找几个点。

函数图像绘制步骤：列表---描点---连线

(1)列表取值时，x≠0，因为x=0函数无意义，为了使描出的点具有代表性，可以以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y值。

(2)由于函数图象的特征还不清楚，尽量多取一些数值，多描一些点，从而便于连线，使画出的图象更精确。

(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线。

因为解析式中，x不能为0，所以y也不能为0，反比例函数的图象不可能与x轴相交，也不可能与y轴相交，但随着x无限增大或是无限减少，函数值无限趋近于0，故图像无限接近于x轴。

涉及交点情况

■ 找交点及交点个数：已知交点的某一横坐标，代入即可求出其纵坐标，反之亦然;当要求交点坐标时，将反比例函数与一次函数联立方程组，进行求解;

■ 求解交点个数：将一次函数和反比例函数联立方程组的解的个数就是交点个数。

■ 求解析式：求解析式一般需要函数图像上的点的坐标，函数图像上有几个未知数，一般需要找几个点。反比例函数的综合应用中，通常寻找交点的坐标，从而得出解析式并分别求得解析式中的常数值。

涉及面积的运用

坐标系中的图形面积问题最基本的图形为三角形，解答核心是要把点坐标转化为线段长度。

▼ 若三角形有一边在坐标轴上，通常以这条边作为三角形的底边。

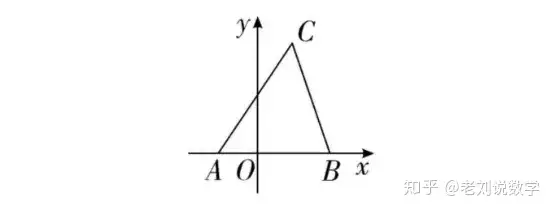
▼ 三边都不在坐标轴上，需要对图形进行割补。

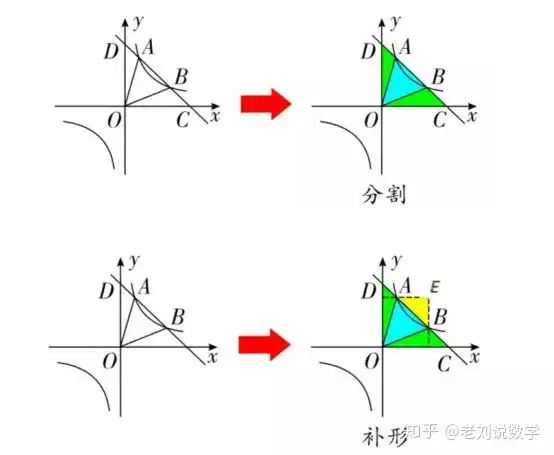
▼ 在前文性质1和2中，我们提到有关反比例函数面积的性质，此外，我们需要了解的是有关反比例函数y=k/x(k为常数且k≠0)中|k|的几何意义：过双曲线上任意一点引x轴、y轴的垂线，所得的矩形面积为|k|。

▼ 如果题目中给出线段比例和四边形的面积求k问题，利用同底等高三角形面积与高之间的关系，以及面积与k之间的关系，求出k。

注意：反比例函数图象是一种特殊的图形，它的两个分支既关于原点对称，又关于直线Y=X、Y=-X对称，因此我们做题时要充分利用反比例函数的对称性来解题。

　　 欢迎使用手机、平板等移动设备访问中考网，2024中考一路陪伴同行！>>点击查看