​2023年初中数学对反比例函数图象性质的深入解读

反比例函数的图象与性质中，教材列举了三个反比例函数y=2/x，y=4/x，y=6/x，要求观察它们的图象，发现它们的共同特征(教材第150页)，同时为了引导学生思考，提出了三个问题：

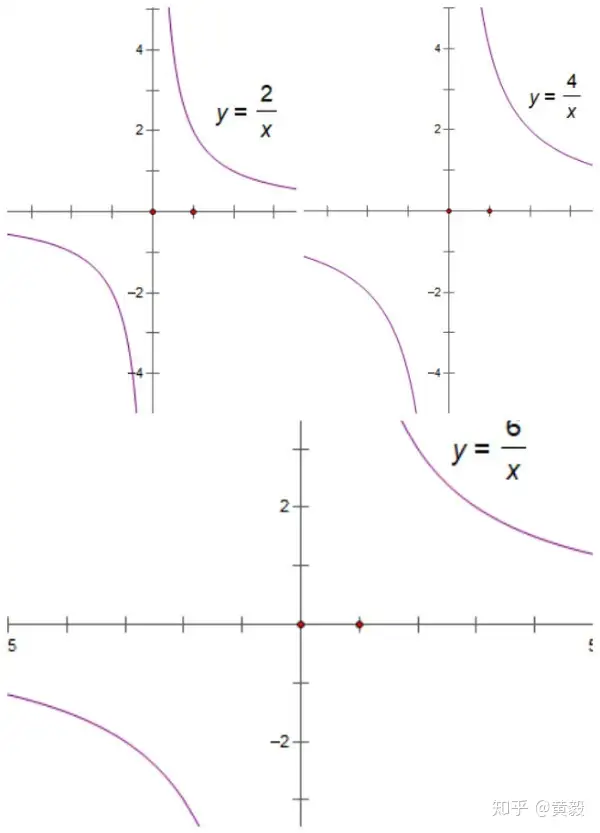
(1)函数图象分别位于哪个象限内?

(2)在每一个象限内，随着x值的增大，y的值是怎样变化的?能说明这是为什么吗?

(3)反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?为什么?

课堂反馈

由于在前一节课中，我们练习过如何绘制反比例函数的图象双曲线，因此本节课的图象是学生在练习本上绘制的，之所以没有采用直接看课本，是为了进一步熟悉双曲线的特点，动手画比仅用眼看要深刻。

绘制过程中，为了让学生方便类比，于是建议在同一个坐标系中画三对双曲线，如下图：

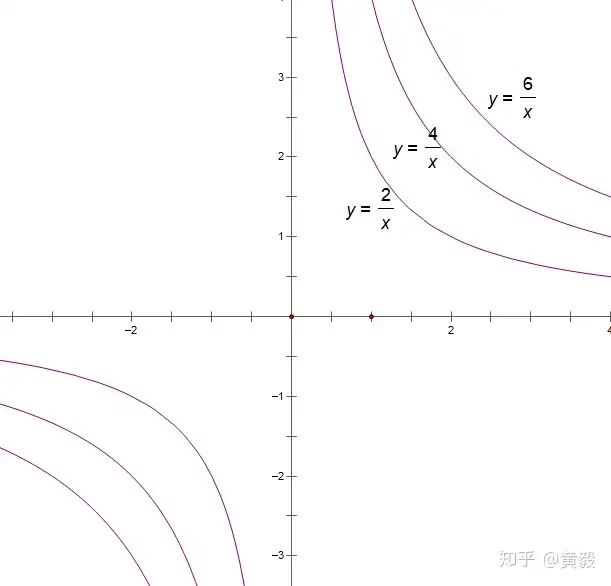
很快，学生能够观察出第一个特征：当k>0时，双曲线在第一、三象限，且关于原点中心对称，关于y=x轴对称;紧接着，第二个特征：在每个象限内，y随x的增大而减少，之所以强制在每个象限内，是因为自变量x不为0，第三个特征：双曲线无限接近坐标轴，这个特征是受问题3启发，毕竟是否与x轴、y轴相交，属于图形直观。

按照教学要求，探索已经圆满完成，无论是课程标准中对反比例函数的要求，还是教参上对此部分内容的要求，均已达到。

课程标准要求：

教参第212页要求：

因此，当学生提出第四个特征的时候，便是对反比例函数图象的深入理解了，即当k越大，双曲线离“中间”越远。

这是一句学生归纳用语，并不十分符合数学语言规范，但是对于这个探索成果，无论如何也不应该否定，因此，需要想办法对它进行数学加工。

学生的意思是k越大，双曲线远离坐标轴，但表述似乎也不对，刚刚探索到的第三条特征中不是说双曲线无限接近坐标轴吗?怎么又远离呢?而事实上，如果观察它们，确定一条比一条更“远”。

我们首先要明确学生的认知范围，在初中阶段，数学上形容远近，是用距离这个概念，而最初的距离，出现在两点之间的线段长度，后来的所有和距离有关的概念，无不是建立在两点之间，例如点到直线的距离，过这一点向直线作垂线段，这点到垂足之间的距离叫点到直线的距离，再例如平行线间的距离，即其中一条直线上的任意点到另一条直线的距离，即使在学习圆之后，点和圆的位置关系时，距离是用点和圆心的距离，等等，基本上，谈到距离，最终都会归结为点与点之间的线段长度。

那么双曲线怎么办?参照原点还是坐标轴?

正因为双曲线与坐标轴是无限接近的关系，并不方便描述，因此，我选择原点为参照，再结合双曲线关于原点中心对称，同时也关于y=x轴对称，将y=x这条对称轴作出来，如下图：

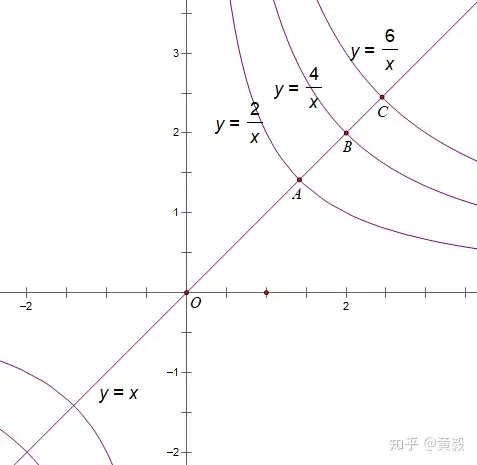
当k>0时，y=x与双曲线y=2/x，y=4/x，y=6/x依次相交于点A、B、C，依然从图形直观上观察，OA

于是，这条特征可以这样描述：定义y=x与反比例函数y=k/x(k>0)第一象限内的分支交点到原点的线段长度为双曲线到原点的距离。此时k越大，双曲线离原点越远。

类似的，对于该双曲线位于第三象限内的描述，依照相同标准，而对于后续的k<0的情况，也适用。

中考真题

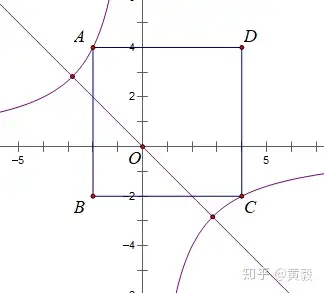
2019年湖北省宜昌市中考数学第24题第1小题，正是考察图形直观，原题如下：

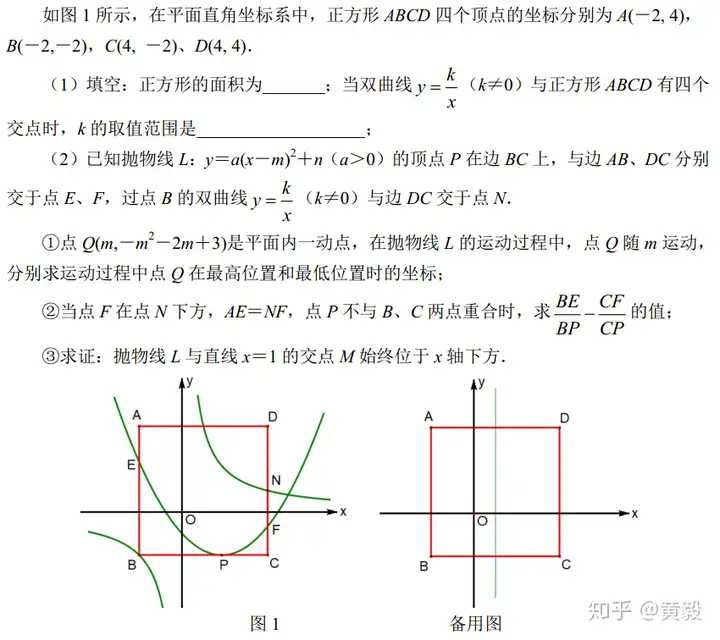
我们看这道题的第1小题第2个空，当双曲线y=k/x与正方形ABCD有四个交点，这句话如何理解?

此题图1中，我们看到了k>0时的一种特殊情况，以此为基准进行动态想像，双曲线经过点B时，与正方形有在个交点，依据反比例函数图象第四个特征，当k增大时，双曲线离原点越来越远，而题中正方形对角线BD恰好是y=x的一部分，因此，k>0时，只要k值比经过点B时小即可，所以0

虽然在k<0时，并没有y=-x进行参照，但我们可以作出这条直线，借助双曲线对称性进行观察，如下图：

教学反思

反比例函数图象特征，并不一定要拘泥于教材，对于双曲线离原点距离这一描述，依然属于反比例函数图象变化。教材中之所以未对此种图象特征进行明文归纳，考虑到初中阶段学生的理解水平，同时这条性质也比较容易通过几何直观得到，所以不作特别要求。

但是在平时教学中，学生面对教师提出的课堂探索要求，多半会有个别人提出来，这时不宜回避，而应该用较为准确的数学语言进行描述。在备课时，也应该充分考虑到教材中所提问题，学生可能的回答。如果仅仅是向学生要求，观察这三条反比例函数图象特征，那么学生思维便不会受太大约束，如果针对教材上三个问题进行提问，便有可能失去探索这一特征的机会。

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看