2023年初中数学知识点：三角形的三条线段

三角形的三条线段

高：三角形的身高

每一个三角形中都有三条高，高与连接的顶点对边存在着垂直的位置关系。根据三角形的分类，我们通过作图的方式可以理解：

(1)锐角三角形的三条高都存在于三角形内;

(2)钝角三角形的三条高不交于一点，只有一=条在三角形内部，另外两条与其延长线相交;

(3)直角三角形的三条高线交于一点，一条高线位于图形内部，其他两条在直角边上。

中线：三角形的重心

(1)每一个三角形内有三条中线，这三条中线的交点叫做“重心”

(2)重心到顶点的距离与重心到对边重点的距离之比为2：1

(3)重心和三角形的顶点组成的三个三角形面积相等

(4)重心到三角形三个顶点的距离平方和最小

(5)在直角坐标系中，重心的坐标是顶点坐标的算术平方根

(6)重心是三角形内到三边距离之积最大的点

角平分线：三角形的内心

(1)每一个三角形也有三条角平分线，这三条角平分线的交点叫做“内心”

(2)内心到三角形三边的距离相等

常见应用类型

类型一：三角形角平分线和高、中线定义的直接应用

该类型主要考察对知识点的掌握能力和运算能力，出题类型主要以选择题和解答题的形式出现，难易程度一般，可直接会根据定义、性质等做出推算。对于高和中线的应用多与角平分线进行结合出题，单独考察时要明晰高和中线的作图方式即可。

如图所示，在△ABC中，D，E，F是BC边上的三点，且∠1=∠2=∠3=∠4，AE是哪个三角形的角平分线( )

A.△ABE B.△ADF

C.△ABC D.△ABC，△ADF

【分析】根据三角形的角平分线的定义得出.

【解答】解：∵∠2=∠3，

∴AE是△ADF的角平分线;

∵∠1=∠2=∠3=∠4，

∴∠1+∠2=∠3+∠4，即∠BAE=∠CAE，

∴AE是△ABC的角平分线。

故选：D。

类型二：三角形的角平分线与高线相结合求角的度数

角平分线与高的结合应用是三条线段中的常见出题类型，通常题目要求算角的大小或者各角进行对比及角之间不等的运用，多以证明题的形式出现。要注意题目给出已知条件，从而分析角平分线、高等要素中关系。

如图，在△ABC中，AD是高，AE是∠BAC的平分线，∠B=70°，∠C=34°，求∠DAE的大小.

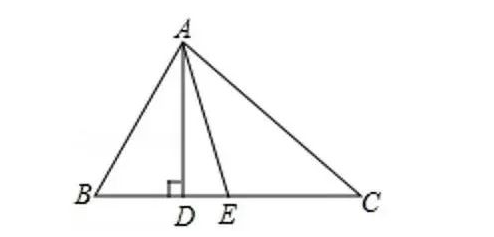
【分析】根据三角形内角和定理求得∠BAC的度数，则∠EAC即可求解，然后在△ACD中，利用三角形内角和定理求得∠DAC的度数，根据∠DAE=∠DAC-∠EAC即可求解.

类型三：求三角形两内角平分线相交所成角的度数

在三角形的三条线段中，角平分线经常作为考点和要点出现在试题中，进行角与角、角与线段、线段与线段之间的比较。

如图，△ABC中，BE，CD为角平分线且交点为点O，当∠A=60°时，

(1)求∠BOC的度数;

(2)当∠A=100°时，求∠BOC的度数;

(3)若∠A=α°时，求∠BOC的度数.

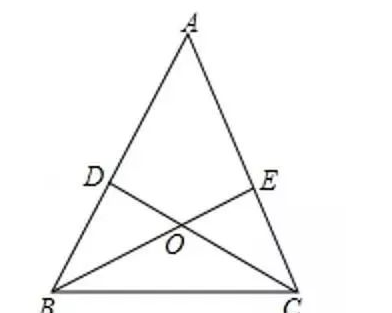
【分析】(1)在△ABC中利用三角形内角和定理和角平分线的定义可求得∠OBC+∠OCB，在△BOC中利用三角形内角和定理可求得∠BOC;(2)方法同(1);(3)方法同(1)。

三角形的重心和内心主要放在有关向量和圆的应用学习中，后续更新将会涉及到详细内容……

数学的学习要全面回归课本，把书上的概念、性质、公式、定理以及衔接知识、拓展知识进行整理、归纳，形成知识网络，然后转化思想，运用到实际的题型中，这才是高效有用的学习方法。

三角形是初中数学中几何部分的基础图形，在牢固掌握基础知识的前提下，要积极探索其中的知识奥秘，这样才能有便于后续其他几何图形的学习和应用。

     编辑推荐：

      2023年中考各科目重点知识汇总

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看