​2023年初中数学：利用对称性质证明几何题

首先，我们来看看例1、如下图所示：

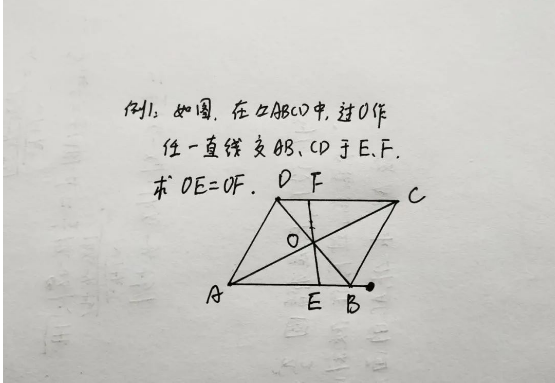
很多学生拿到本题时，基本上都能做出来，而且都是用同一个方法——通过两个三角形全等，得出对应线段相等，其过程如下图所示：

这样的做法是通法，但是我们只要多挖掘题目的意思，就能得到更有用的信息：平行四边形是中心对称图形，利用中心对称图形的性质，便能得到更简单明了的方法，如下图所示：

当然了，这样的做法必须要求我们平时上课时，要对对称性质的重视，在实际教学中，很多学生只会利用其画图，而忽视也可以利用它解题。

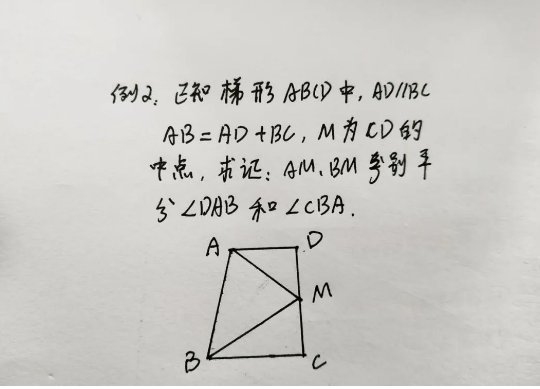
再来看看例2、如下图所示：

这道题相对来说难一点了，不过很多学生还是能够用这样的方法做出来：通过作辅助线，找到两个三角形全等，得出对应角相等，再进行等量代换，即可证明出来结论了，步骤如下图所示：

对本次，我们也可以换一种思维去思考：整个图形是一个梯形，可以根据中心对称图形得出另一个和它全等的梯形，而这两个梯形恰好组成一个平行四边形，利用已知条件证得其为菱形，得出最后结论，如下图所示：

此题的难点就是：我们是否能够找到某一点，以它为对称中心，构造中心对称图形。

轴对称和中心对称在初中数学中，占比不高，而且很简单，往往就是因为这样的原因，我们在解决几何图形时，很少能够重视它，运用它去解题。更多的是模范老师的解法，不断地进行解题训练，从而造成思维定势，不利于数学几何的学习。

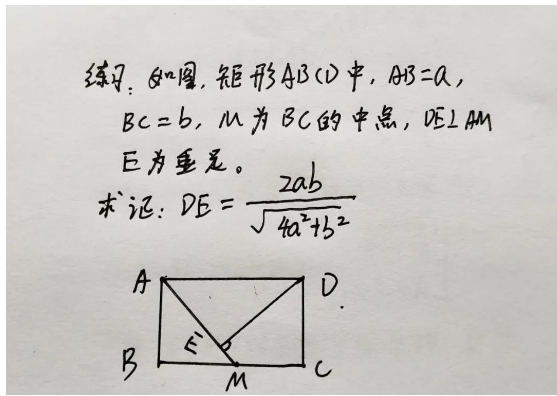
最后，留一道中考题，读者们可以先用通用解法，再利用对称性质来解，看看哪个方法对你来说更容易理解，题目如下图所示：

最后，以上都是本人如何利用对称性质解题的一些浅陋之见，耐本人能力眼界有限，有不当之处，还望读者不吝赐教。

     编辑推荐：

      2023年中考各科目重点知识汇总

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看