2023年初中数学平面直角坐标系常考题型四

规律探究

以循环为特征的规律探索型问题，解决此类问题应先观察图形的变化趋势，然后对第一个图形进行分析，运用从特殊到一般的探索方式，如果以m次为一个循环，那么第n次的情形与n÷m的余数是相同的，整除时与最后一次情形相同。

例题5：如图，直角坐标平面xOy内，动点P按图中箭头所示方向依次运动，第1次从点(-1，0)运动到点(0，1)，第2次运动到点(1，0)，第3次运动到点(2，-2)，…按这样的运动规律，动点P第2020次运动到点( )

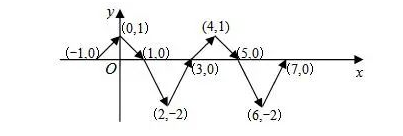
分析：观察图形可知，每4次运动为一个循环组循环，并且每一个循环组向右运动4个单位，用2020除以4，然后根据商和余数的情况确定运动后点的坐标即可.

解：∵2020÷4=505，

∴动点P第2020次运动为第505个循环组的第4次运动，横坐标505×4-1=2019，纵坐标为0，

∴点P此时坐标为(2019，0).

平面直角坐标系下的规律探究题，解答时注意探究动点的运动规律，又要注意动点的坐标的象限符号。

     编辑推荐：

      2023年中考各科目重点知识汇总

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看