2023年初中数学平行四边形常见题型分析二

例题2：如图，已知四边形ABCD和四边形ADEF均为平行四边形，点B，C，F，E在同一直线上，AF交CD于O，若BC=10，AO=FO，求CE的长。

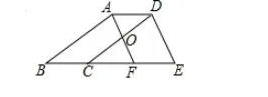
分析：根据平行四边形的性质得出AD=BC=EF，AD∥BE，从而得到∠DAO=∠CFO，再加上对顶角相等，可以得到△AOD≌△FOC，根据全等三角形的性质得到AD=CF，即AD=BC=EF=CF，从而得到线段CE的长度。也可以借助中位线定理解决。

（2）求线段（边或对角线）的取值范围

解：∵四边形ABCD和四边形ADEF均为平行四边形，∴AD=BC，AD=FE，AD∥BE，AF∥DE，∴AD=BC=FE=10，∵AF∥DE，AO=FO，∴CF=FE=10，∴CE=10+10=20

例题3：在平行四边形ABCD中，AB=4，BC=6，对角线AC、BD相交于点O，则OA的取值范围是多少？

分析：由AB=4，BC=6，利用三角形的三边关系，即可求得2

（3）利用平行四边形的性质证明角相等、边相等和直线平行

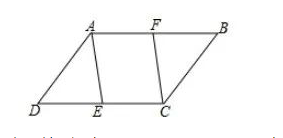
分析：由四边形ABCD为平行四边形可得：AB=CD，AB∥CD。由已知条件DE=BF，根据等边减等边可得AF=CE，由此可证明四边形AECF为平行四边形，从而得到AE∥CF。通过此题可知，平行四边形又为我们证明直线平行增加了一种方法。

证明：∵四边形ABCD为平行四边形，∴AB∥CD，AB=CD又∵DE=BF，∴AB-BF=CD-DE，即AF=CE∴四边形AECF为平行四边形，∴AE∥CF

     编辑推荐：

      2023年中考各科目重点知识汇总

　　 欢迎使用手机、平板等移动设备访问中考网，2024中考一路陪伴同行！>>点击查看