初中数学难点：平行四边形的存在性问题破解策略

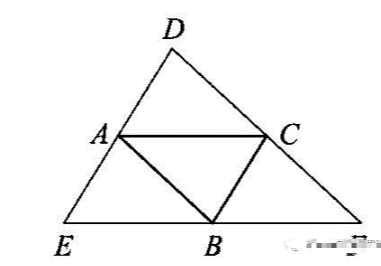
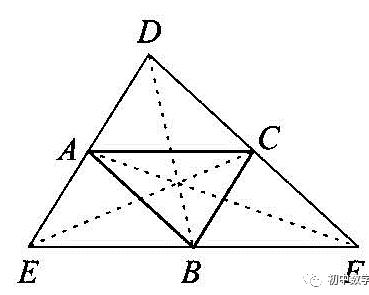
这类题，一般有两个类型：(1)“三个定点、一个动点”的平行四边形存在性问题：以A,B,C三点为顶点的平行四边形构造方法有：①作平行线：如图，连结AB,BC,AC，分别过点A,B,C作其对边的平行线，兰条直线的交点为D,E,F，则四边形ABCD,ACBE,ABFC均为平行四边形.

②倍长中线：如图，延长边AC,AB,BC上的中线，使延长部分与中线相等，得点D,E,F，连结DE,EF,FD，则四边形ABCD,ACEE ,ABFC均为平行四边形.

(2)“两个定点、两个动点”的平行四边形存在性问题：先确定其中一个动点的位置，转化为“三个定点、一个动点”的平行四边形存在性问题，再构造平行四边形.解平行四边形存在性问题，无论是以上哪种类型，若没有指定四边形顶点顺序，都需要分类讨论.

通常这类问题的解题策略有：

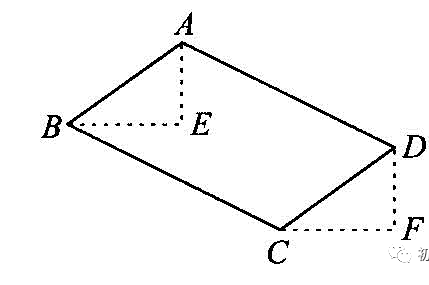
(1)几何法：先分类，再画出平行四边形，然后根据平行四边形的性质来解答.如图，若AB//CD且AB=CD，过B,C作一组平行线BE,CF，过A,D作一组平行线AE,DF，则DAEB且DDFC，从而得到线段间的关系式解决问题

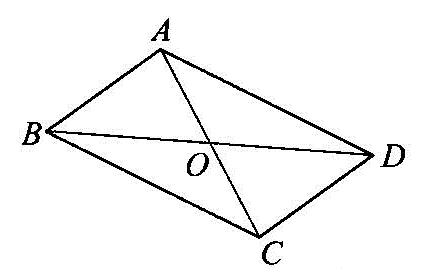
(2)代数法：先罗列四个顶点的坐标，再分类讨论列方程，然后解方程并检验.如图，已知平行四边形ABCD，连结AC,BD交于点。-设顶点坐标为A(xA•YA) ,B(xB •YB) ,C(xc, Ye) ,D(xo ,yo).

【典型例题1】

【答案解析】解：

【典型例题2】

【答案解析】解：

　　 欢迎使用手机、平板等移动设备访问中考网，2024中考一路陪伴同行！>>点击查看