来源:网络资源 2023-04-09 20:00:31
如果你也想进入数据分析的领域,那么统计学知识和概率论知识是必不可少的理论,虽然短时间你会觉得这个对码代码来说没有什么用处,但是这个基础还是要打好的,磨刀不误砍柴工。
一、描述性统计
我想起了大学时候读过,后期接触专业课的时候反而不熟了。小学的时候都接触过的平均数,标准差等等,我们真的有细细品味过其内涵吗?
1.平均数
这个概念很简单,一组数据的平均水平,但是平均数发现不了这组数据中“鹤立鸡群”的数字。一个100分的学霸和4个70分的普通人平均一下,5个人的平均水平是76分,这无疑是对学霸的“亵渎”,也没有办法发现这个“骨骼惊奇”的人类了。
2.中位数、众数、四分位数、箱线图、直方图
中位数可以发现这组数据的中间水平,众数即为大众水平,四分位数得到的箱线图和中位数结合来看,可以得到大部分人的水平,以及优劣的集中程度。
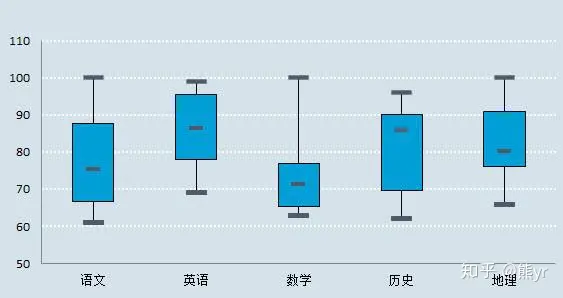
如上图,数学箱线图里我们可以看出这个班级数学最高分有100,最低分63左右,历史最高分不到100,最低分低于数学。但是我们能说历史的成绩要不如数学吗?数学的箱体偏下,中位数居中,说明数学虽然有100的学霸,但优秀者凤毛麟角,一半人还是处于80到60 之间。而历史成绩,则在98到62范围内更均匀,而且中位数88左右在箱体偏上部分,说明有一半人在88以上,88到90的人有四分之一。同理对于地理来说虽然中间部分集中情况优于数学,但是四分之一的人集中在76到80,明显不见得比历史好。
箱线图相当于是中位数、众数、四分位数在图像上更为直观的反映,因为我们大脑对于图像理解更为快速。箱线图可以让那些“凤毛麟角”凸显出来,相比于平均数更能凸显异常者。
(这里想请教一下MAC版EXCEL2016怎么画箱线图,怎么用股价图来画)
直方图也是差不多的用途,直方图在数据上更为精确,能够通过频率和范围直接计算出频数,而箱线图则表示不出来,而且直方图能更直观的感受数据的分布情况。但是直方图在多组数据同时表示时则相对来说比较复杂,一组数据需要一个直方图,箱线图则不会占据较大的篇幅。
3.标准差、夏普比率
标准差,大家都能理解就是稳定程度。作为一个金融渣,时隔几年终于深层次理解了曾经投资课听不懂的夏普比率,这说明我确实没有自己想象的那么学霸。
如果我们不是靠背诵知道的标准差代表稳定程度,仅仅从公式理解上,即为这一组数据里每一个数字与平均值的差距。那么在投资上代表风险,即为某一种投资,相对于平均值我可能赔也可能赚。那么再来理解夏普比率,某一种投资组合的投资回报减去无风险回报后的溢价与标准差的比值。假如夏普比率为0.5,意思是我在赚0.5份溢价的时候可能承担的风险是赚1份或者赔1份的风险。(鄙人粗见,欢迎指正)
4.标准分

表示离平均值的差距是标准差的几倍。我是这么理解的:全体考生的标准差相当于全体考生的集散程度,而个体的标准分相当于这个个体偏离“组织”的程度。如果整体的标准差很大,我即使偏离平均很多,我也不见得离组织很远,因为大家都离得远。但是如果整体标准差不大,我如果稍微比平均值差一些很可能就偏离组织了。标准分的正负说明我是在平均以上还是以下,标准分的绝对值说明我离“组织”的距离相对于整个组织的离散程度是更离散还是还好。
标准分和标准差的区别在于标准差是整体的离散程度,而标准分是针对个体的离散程度和整体离散程度的相对效果。
二、概率
1.乘法公式
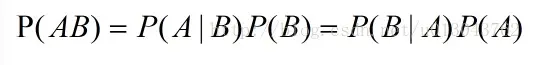
第一个是乘法公式,第二个是条件概率公式。
当且仅当两个随机事件A与B满足P(A∩B)=P(A)P(B)。
2.全概率公式

3.贝叶斯公式
![]()
贝叶斯公式的理解:假设i=2,我们知道有两种方法以及选择每种方法的概率,同时我们知道每种方法都会导致结果B且只有这两种方法会导致结果B,我们又知道两种方法分别导致结果B的概率。现在结果B出现了,我们怎么确定某一种方法导致结果B的概率。这里先验概率就是已知条件,后验概率就是结果出现后我们想知道这个结果由某一种方法导致的概率。
4.大树定律
当统计数量足够大,那么事物出现的频率就能无限接近他的期望。如果数量很小,那么事物出现与其期望值一点关系都没有。
三、决策树分析目前个人工作情况
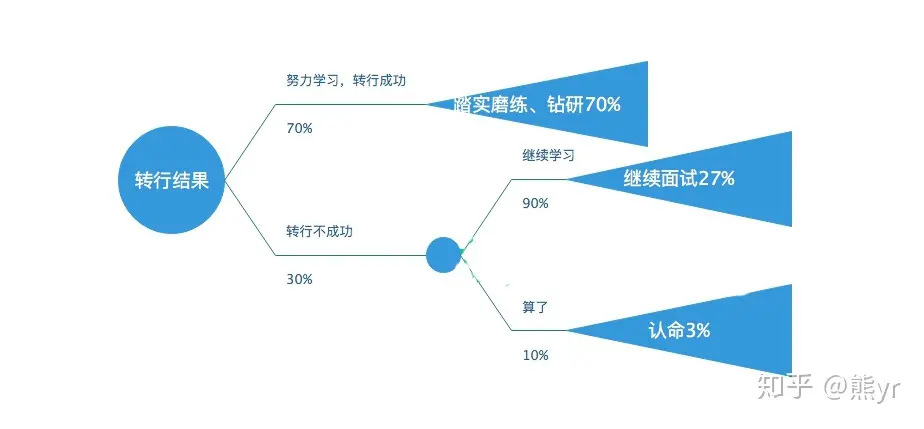
鉴于本人对于目前工作情况并不满意,原因主要是三个:一、我需要一个有双休的工作,工作时间不规律让我很不适应,身体素质也因为忙碌的三个月下降了不少。二、我性格不适合营销,我喜欢不停的钻研,自己思考,作出成果。三、目前公司的文化不认同。所以我没有什么是否需要转行的考虑。只有是否能转行成功的考虑,我很怕因为年龄和经验的问题而不被认可。但是基于我对公司的认同度的极速下滑,我还是有必要转行。但是目前困难已经出现了,我搜索引擎使用的不是很好,特别是爬虫翻墙挖掘数据有一定的困难。另外MAC版的软件用起来和window还是差别很大,不是很方便。
编辑推荐:

欢迎使用手机、平板等移动设备访问中考网,2025中考一路陪伴同行!>>点击查看