来源:网络资源 2023-08-23 19:17:53
第六章:函数及其图像
一、平面直角坐标系
1、平面内有公共原点且互相垂直的两条数轴,构成平面直角坐标系。
在平面直角坐标系内的点和有序实数对之间建立了一一对应的关系。
2、不同位置点的坐标的特征:
3.点P(x,y)坐标的几何意义:
(1)各象限内点的坐标有如下特征:点P(x,y)在第一象限←→x>0,y>0;点P(x,y)在第二象限←→x<0,y>0;点P(x,y)在第三象限←→x<0,y<0;点P(x,y)在第四象限←→x>0,y<0。(2)坐标轴上的点有如下特征:点P(x,y)在x轴上台y为0,x为任意实数。点P(x,y)在y轴上一x为0,y为任意实数。(1)点P(x,y)到x轴的距离是∣y∣;(2)点P(x,y)到y袖的距离是∣x∣;(3)点P(x,y)到原点的距离是√(x2+y2)(1)点P(a,b)关于x轴的对称点是P1(a,-b);(2)点P(a,b)关于y轴的对称点是P2(-a,b);(3)点P(a,b)关于原点的对称点是P3(-a,-b);
二、函数的概念
1、常量和变量:
在某一变化过程中可以取不同数值的量叫做变量;保持数值不变的量叫做常量。
2、函数:
一般地,设在某一变化过程中有两个变量x和y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数。
(1)自变量取值范围的确是:
①解析式是只含有一个自变量的整式的函数,自变量取值范围是全体实数。
②解析式是只含有一个自变量的分式的函数,自变量取值范围是使分母不为0的实数。
③解析式是只含有一个自变量的偶次根式的函数,自变量取值范围是使被开方数非负的实数。
注意:
在确定函数中自变量的取值范围时,如果遇到实际问题,还必须使实际问题有意义。
(2)函数值:
给自变量在取值范围内的一个值所求得的函数的对应值。
(3)函数的表示方法:
①解析法;②列表法;③图像法
(4)由函数的解析式作函数的图像,一般步骤是:
①列表;②描点;③连线。
三、几种特殊的函数
1、一次函数:

直线位置与k,b的关系:
(1)k>0直线向上的方向与x轴的正方向所形成的夹角为锐角;
(2)k<0直线向上的方向与x轴的正方向所形成的夹角为钝角;
(3)b>0直线与y轴交点在x轴的上方;
(4)b=0直线过原点;
(5)b<0直线与y轴交点在x轴的下方;
2、二次函数:
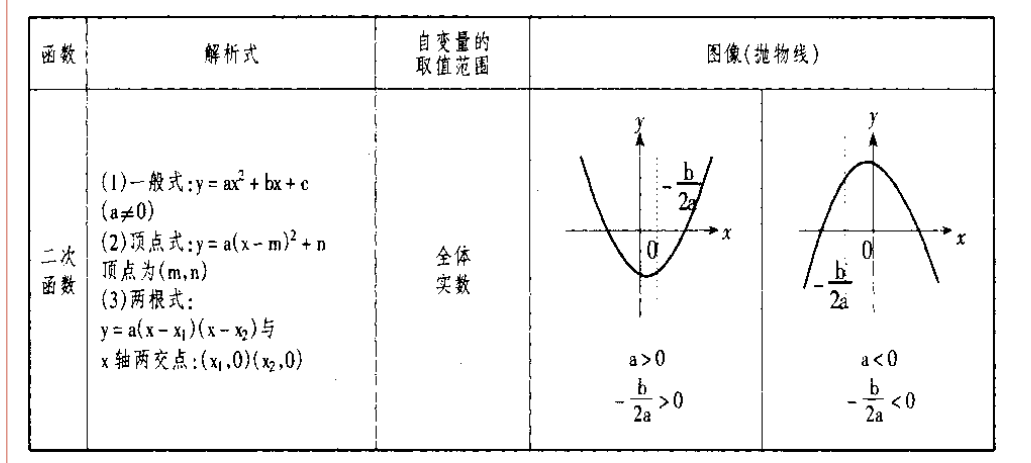
抛物线位置与a,b,c的关系:
(1)a决定抛物线的开口方向
a>0←→开口向上;
a<0←→开口向下。
(2)c决定抛物线与y轴交点的位置:
c>0←→图像与y轴交点在x轴上方;
c=0←→图像过原点;
c<0←→图像与y轴交点在x轴下方。
(3)a,b决定抛物线对称轴的位置:
a,b同号,对称轴在y轴左侧;
b=0,对称轴是y轴;
a,b异号,对称轴在y轴右侧。
3、反比例函数:
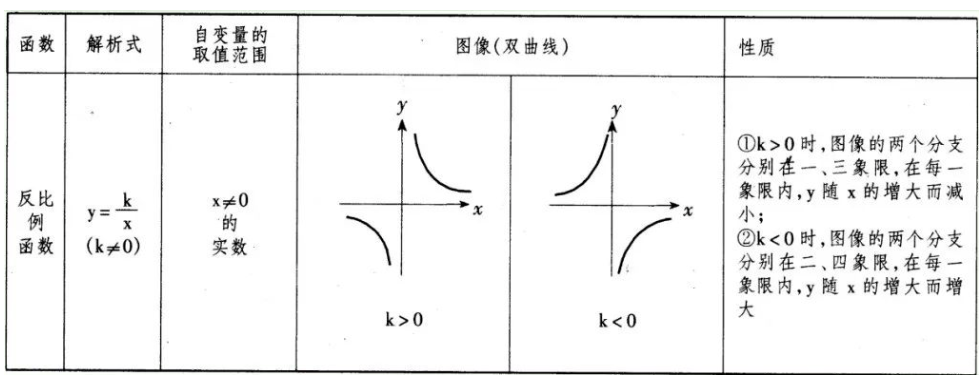
4、正比例函数与反比例函数的对照表:

编辑推荐:

欢迎使用手机、平板等移动设备访问中考网,2024中考一路陪伴同行!>>点击查看