2024年初中数学知识点精粹梳理：圆的定理

简单对圆的部分定理知识点进行梳理。

垂径定理

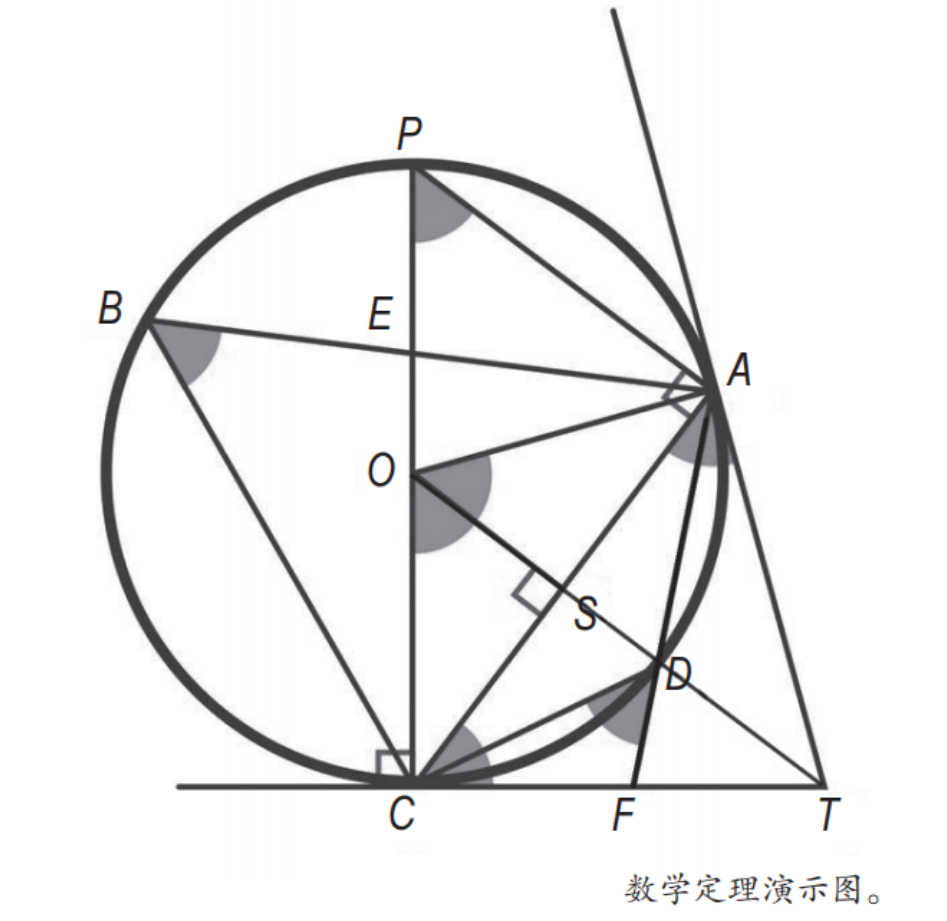
垂直于弦的直径平分弦，且平分这条弦所对的两条弧。如图，观察 OD、CA，以及弦 CD、AD 即可得出上述结论。

推导定理：

平分弦(不是直径)的直径垂直于弦，而且平分弦所对的两段弧。弦的垂直平分线经过圆心，并且平分这条弦所对的弧。平分弦所对的一条弧的直径垂直平分这条弦，并且平分这条弦所对的另一条弧。在同圆或者等圆中，两条平行弦所夹的弧相等。

切线长定理

从圆外一点到圆的两条切线的长相等，这个点与圆心的连线平分切线的夹角。如图，观察 TC、TA 即可得出上述结论。

切线的性质：

切线和圆只有一个公共点 ;切点和圆心的距离等于圆的半径 ;切线垂直于经过切点的半径 ;经过圆心垂直于切线的直线必过切点;经过切点垂直于切线的直线必过圆心。

切线的判定方法：

如果直线与圆只有一个公共点，这时直线与圆的位置关系叫作相切，这条直线叫作圆的切线，这个公共点叫作切点。

割线定理

从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。如图，假设过 F 点的另一条割线为 FA′，那么同理有 FC2=FA′·FD′，又因为 FC2=FA·FD，所以 FA′·FD′=FA·FD，即 F 点到每条割线与圆的交点的两条线段长的积相等。

圆心角定理

在同圆或等圆中，相等的圆心角所对弧相等，所对的弦也相等，所对的弦的弦心距相等。如图，观察∠ B、∠ P、∠ AOC、 、弦 AC、弦心距 OS，即可得出上述结论。

推论：

在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等，那么它们所对应的其余各组量都相等。

圆周角定理

同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的一半。如图，观察∠ B、∠ P 和∠ AOC 即可得出 ：∠ B= ∠ P=1/2 ∠ AOC。

推论：

同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等;半圆或直径所对的圆周角是直角，90°的圆周角所正对的弦的直径;圆内接四边形的对角互补;如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

       编辑推荐：

       2024年中考各科目重点知识汇总

　　 欢迎使用手机、平板等移动设备访问中考网，2023中考一路陪伴同行！>>点击查看